Hierarchical regularization networks for sparsification based learning on noisy datasets
Paper and Code
Jun 09, 2020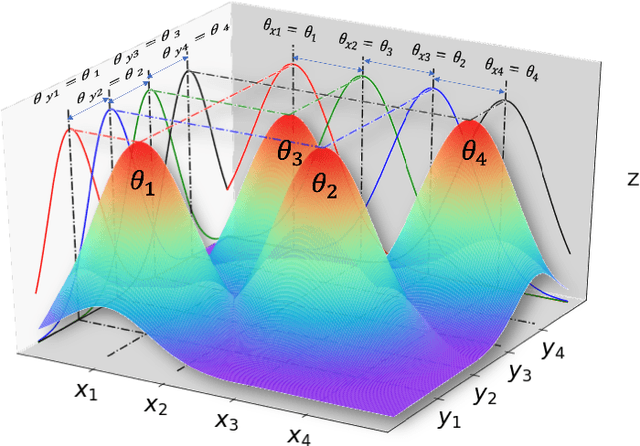
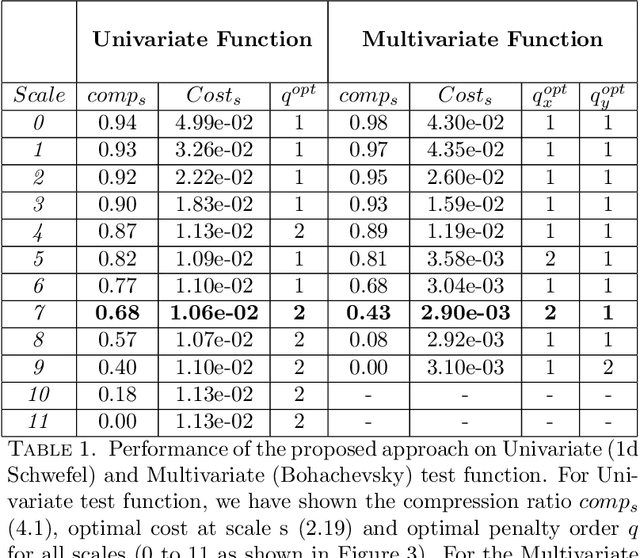
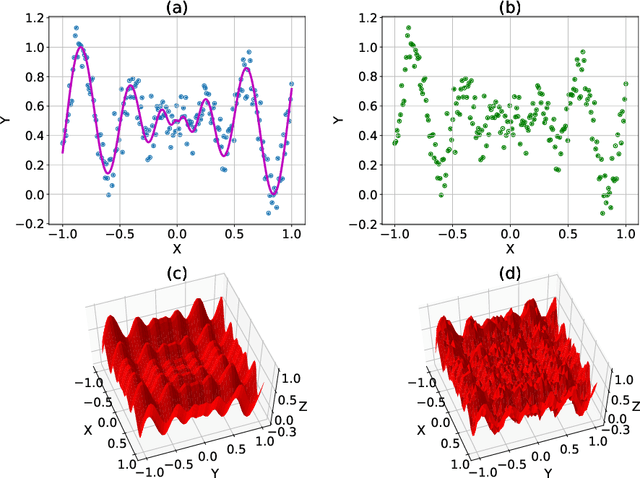

We propose a hierarchical learning strategy aimed at generating sparse representations and associated models for large noisy datasets. The hierarchy follows from approximation spaces identified at successively finer scales. For promoting model generalization at each scale, we also introduce a novel, projection based penalty operator across multiple dimension, using permutation operators for incorporating proximity and ordering information. The paper presents a detailed analysis of approximation properties in the reconstruction Reproducing Kernel Hilbert Spaces (RKHS) with emphasis on optimality and consistency of predictions and behavior of error functionals associated with the produced sparse representations. Results show the performance of the approach as a data reduction and modeling strategy on both synthetic (univariate and multivariate) and real datasets (time series). The sparse model for the test datasets, generated by the presented approach, is also shown to efficiently reconstruct the underlying process and preserve generalizability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge