A Forward Backward Greedy approach for Sparse Multiscale Learning
Paper and Code
Feb 14, 2021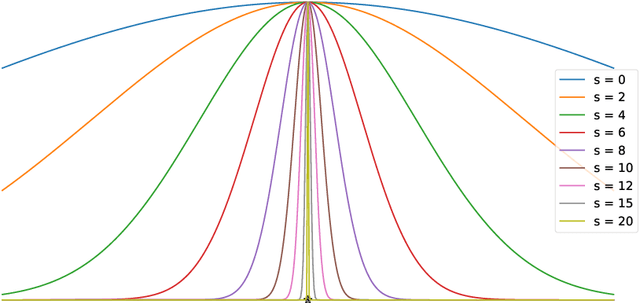
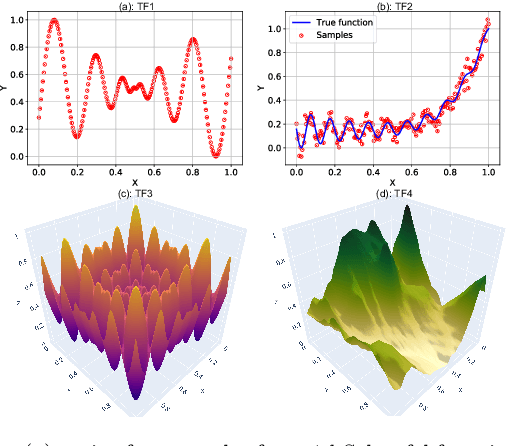
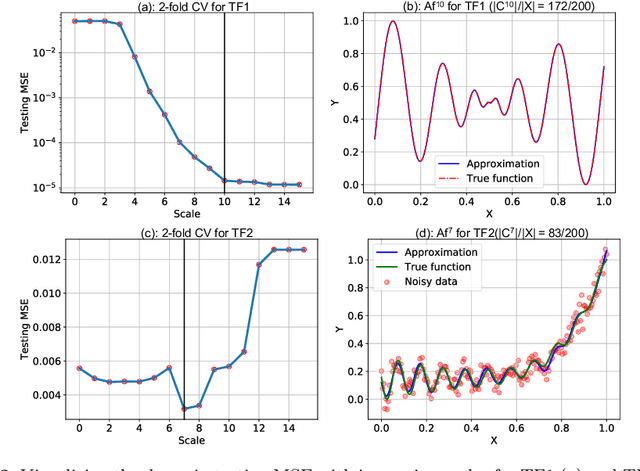
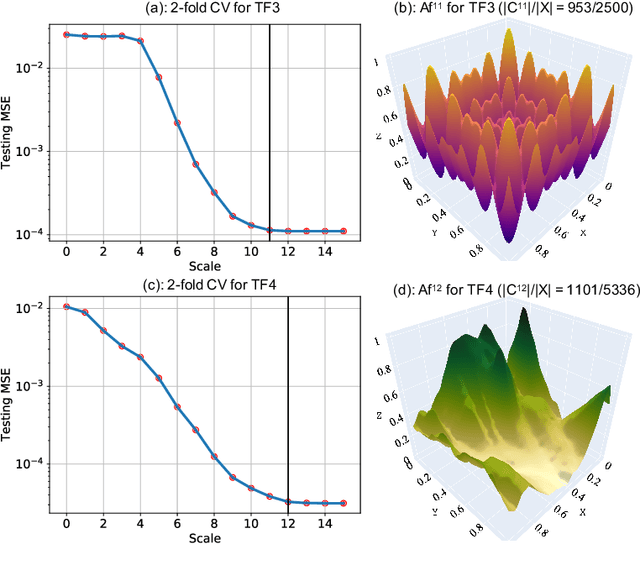
Multiscale Models are known to be successful in uncovering and analyzing the structures in data at different resolutions. In the current work we propose a feature driven Reproducing Kernel Hilbert space (RKHS), for which the associated kernel has a weighted multiscale structure. For generating approximations in this space, we provide a practical forward-backward algorithm that is shown to greedily construct a set of basis functions having a multiscale structure, while also creating sparse representations from the given data set, making representations and predictions very efficient. We provide a detailed analysis of the algorithm including recommendations for selecting algorithmic hyper-parameters and estimating probabilistic rates of convergence at individual scales. Then we extend this analysis to multiscale setting, studying the effects of finite scale truncation and quality of solution in the inherent RKHS. In the last section, we analyze the performance of the approach on a variety of simulation and real data sets, thereby justifying the efficiency claims in terms of model quality and data reduction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge