How Much More Data Do I Need? Estimating Requirements for Downstream Tasks
Paper and Code
Jul 13, 2022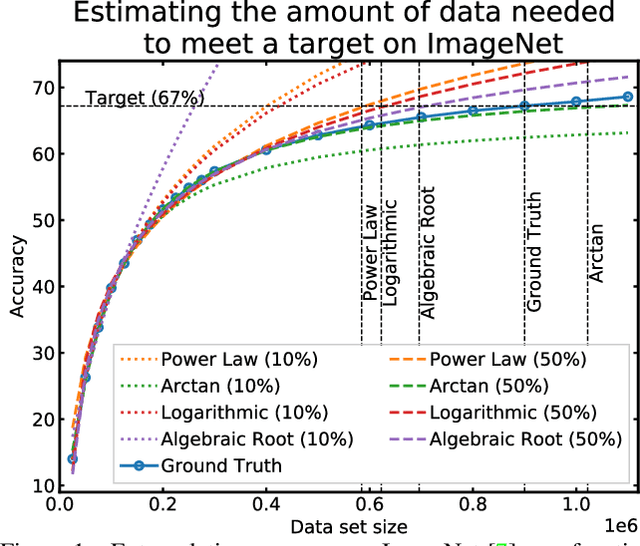

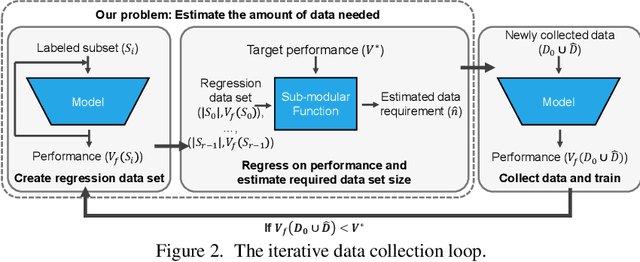
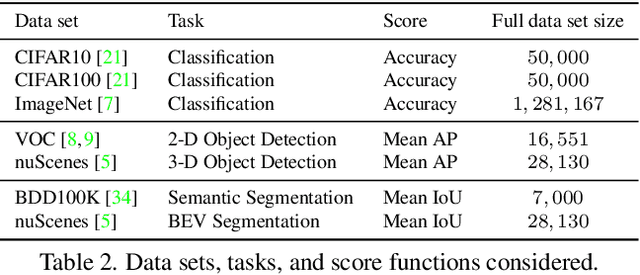
Given a small training data set and a learning algorithm, how much more data is necessary to reach a target validation or test performance? This question is of critical importance in applications such as autonomous driving or medical imaging where collecting data is expensive and time-consuming. Overestimating or underestimating data requirements incurs substantial costs that could be avoided with an adequate budget. Prior work on neural scaling laws suggest that the power-law function can fit the validation performance curve and extrapolate it to larger data set sizes. We find that this does not immediately translate to the more difficult downstream task of estimating the required data set size to meet a target performance. In this work, we consider a broad class of computer vision tasks and systematically investigate a family of functions that generalize the power-law function to allow for better estimation of data requirements. Finally, we show that incorporating a tuned correction factor and collecting over multiple rounds significantly improves the performance of the data estimators. Using our guidelines, practitioners can accurately estimate data requirements of machine learning systems to gain savings in both development time and data acquisition costs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge