Hyp-UML: Hyperbolic Image Retrieval with Uncertainty-aware Metric Learning

Metric learning plays a critical role in training image retrieval and classification. It is also a key algorithm in representation learning, e.g., for feature learning and its alignment in metric space. Hyperbolic embedding has been recently developed. Compared to the conventional Euclidean embedding in most of the previously developed models, Hyperbolic embedding can be more effective in representing the hierarchical data structure. Second, uncertainty estimation/measurement is a long-lasting challenge in artificial intelligence. Successful uncertainty estimation can improve a machine learning model's performance, robustness, and security. In Hyperbolic space, uncertainty measurement is at least with equivalent, if not more, critical importance. In this paper, we develop a Hyperbolic image embedding with uncertainty-aware metric learning for image retrieval. We call our method Hyp-UML: Hyperbolic Uncertainty-aware Metric Learning. Our contribution are threefold: we propose an image embedding algorithm based on Hyperbolic space, with their corresponding uncertainty value; we propose two types of uncertainty-aware metric learning, for the popular Contrastive learning and conventional margin-based metric learning, respectively. We perform extensive experimental validations to prove that the proposed algorithm can achieve state-of-the-art results among related methods. The comprehensive ablation study validates the effectiveness of each component of the proposed algorithm.

Deep Variational Luenberger-type Observer for Stochastic Video Prediction

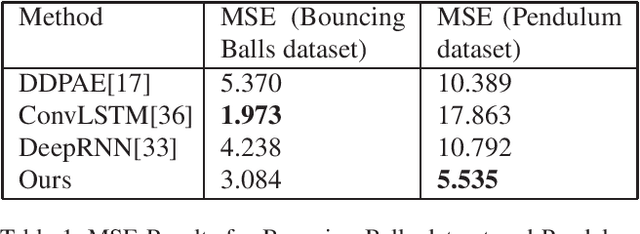
Considering the inherent stochasticity and uncertainty, predicting future video frames is exceptionally challenging. In this work, we study the problem of video prediction by combining interpretability of stochastic state space models and representation learning of deep neural networks. Our model builds upon an variational encoder which transforms the input video into a latent feature space and a Luenberger-type observer which captures the dynamic evolution of the latent features. This enables the decomposition of videos into static features and dynamics in an unsupervised manner. By deriving the stability theory of the nonlinear Luenberger-type observer, the hidden states in the feature space become insensitive with respect to the initial values, which improves the robustness of the overall model. Furthermore, the variational lower bound on the data log-likelihood can be derived to obtain the tractable posterior prediction distribution based on the variational principle. Finally, the experiments such as the Bouncing Balls dataset and the Pendulum dataset are provided to demonstrate the proposed model outperforms concurrent works.