IDEAL: Independent Domain Embedding Augmentation Learning

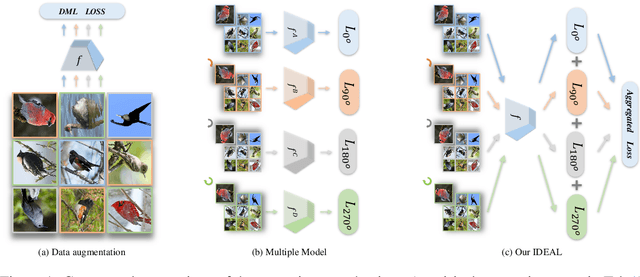
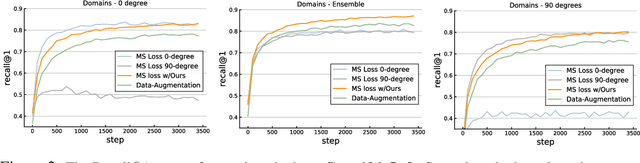
Many efforts have been devoted to designing sampling, mining, and weighting strategies in high-level deep metric learning (DML) loss objectives. However, little attention has been paid to low-level but essential data transformation. In this paper, we develop a novel mechanism, the independent domain embedding augmentation learning ({IDEAL}) method. It can simultaneously learn multiple independent embedding spaces for multiple domains generated by predefined data transformations. Our IDEAL is orthogonal to existing DML techniques and can be seamlessly combined with prior DML approaches for enhanced performance. Empirical results on visual retrieval tasks demonstrate the superiority of the proposed method. For example, the IDEAL improves the performance of MS loss by a large margin, 84.5\% $\rightarrow$ 87.1\% on Cars-196, and 65.8\% $\rightarrow$ 69.5\% on CUB-200 at Recall$@1$. Our IDEAL with MS loss also achieves the new state-of-the-art performance on three image retrieval benchmarks, \ie, \emph{Cars-196}, \emph{CUB-200}, and \emph{SOP}. It outperforms the most recent DML approaches, such as Circle loss and XBM, significantly. The source code and pre-trained models of our method will be available at\emph{\url{https://github.com/emdata-ailab/IDEAL}}.

Deep Variational Luenberger-type Observer for Stochastic Video Prediction

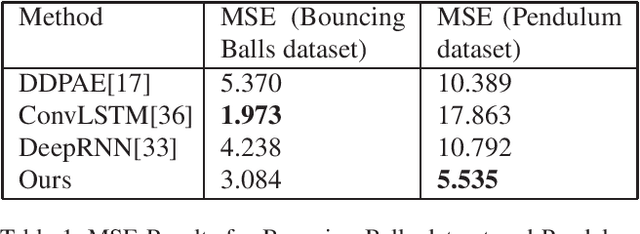
Considering the inherent stochasticity and uncertainty, predicting future video frames is exceptionally challenging. In this work, we study the problem of video prediction by combining interpretability of stochastic state space models and representation learning of deep neural networks. Our model builds upon an variational encoder which transforms the input video into a latent feature space and a Luenberger-type observer which captures the dynamic evolution of the latent features. This enables the decomposition of videos into static features and dynamics in an unsupervised manner. By deriving the stability theory of the nonlinear Luenberger-type observer, the hidden states in the feature space become insensitive with respect to the initial values, which improves the robustness of the overall model. Furthermore, the variational lower bound on the data log-likelihood can be derived to obtain the tractable posterior prediction distribution based on the variational principle. Finally, the experiments such as the Bouncing Balls dataset and the Pendulum dataset are provided to demonstrate the proposed model outperforms concurrent works.