Generative Topological Networks

Generative models have seen significant advancements in recent years, yet often remain challenging and costly to train and use. We introduce Generative Topological Networks (GTNs) -- a new class of generative models that addresses these shortcomings. GTNs are trained deterministically using a simple supervised learning approach grounded in topology theory. GTNs are fast to train, and require only a single forward pass in a standard feedforward neural network to generate samples. We demonstrate the strengths of GTNs in several datasets, including MNIST, celebA and the Hands and Palm Images dataset. Finally, the theory behind GTNs offers insights into how to train generative models for improved performance.

Tighter Bounds on the Information Bottleneck with Application to Deep Learning

Deep Neural Nets (DNNs) learn latent representations induced by their downstream task, objective function, and other parameters. The quality of the learned representations impacts the DNN's generalization ability and the coherence of the emerging latent space. The Information Bottleneck (IB) provides a hypothetically optimal framework for data modeling, yet it is often intractable. Recent efforts combined DNNs with the IB by applying VAE-inspired variational methods to approximate bounds on mutual information, resulting in improved robustness to adversarial attacks. This work introduces a new and tighter variational bound for the IB, improving performance of previous IB-inspired DNNs. These advancements strengthen the case for the IB and its variational approximations as a data modeling framework, and provide a simple method to significantly enhance the adversarial robustness of classifier DNNs.

Faithful Autoencoder Interpolation by Shaping the Latent Space

One of the fascinating properties of deep learning is the ability of the network to reveal the underlying factors characterizing elements in datasets of different types. Autoencoders represent an effective approach for computing these factors. Autoencoders have been studied in the context of their ability to interpolate between data points by decoding mixed latent vectors. However, this interpolation often incorporates disrupting artifacts or produces unrealistic images during reconstruction. We argue that these incongruities are due to the manifold structure of the latent space where interpolated latent vectors deviate from the data manifold. In this paper, we propose a regularization technique that shapes the latent space following the manifold assumption while enforcing the manifold to be smooth and convex. This regularization enables faithful interpolation between data points and can be used as a general regularization as well for avoiding overfitting and constraining the model complexity.

On the Sample Complexity of Learning Bayesian Networks

In recent years there has been an increasing interest in learning Bayesian networks from data. One of the most effective methods for learning such networks is based on the minimum description length (MDL) principle. Previous work has shown that this learning procedure is asymptotically successful: with probability one, it will converge to the target distribution, given a sufficient number of samples. However, the rate of this convergence has been hitherto unknown. In this work we examine the sample complexity of MDL based learning procedures for Bayesian networks. We show that the number of samples needed to learn an epsilon-close approximation (in terms of entropy distance) with confidence delta is O((1/epsilon)^(4/3)log(1/epsilon)log(1/delta)loglog (1/delta)). This means that the sample complexity is a low-order polynomial in the error threshold and sub-linear in the confidence bound. We also discuss how the constants in this term depend on the complexity of the target distribution. Finally, we address questions of asymptotic minimality and propose a method for using the sample complexity results to speed up the learning process.

A Distance-Based Branch and Bound Feature Selection Algorithm

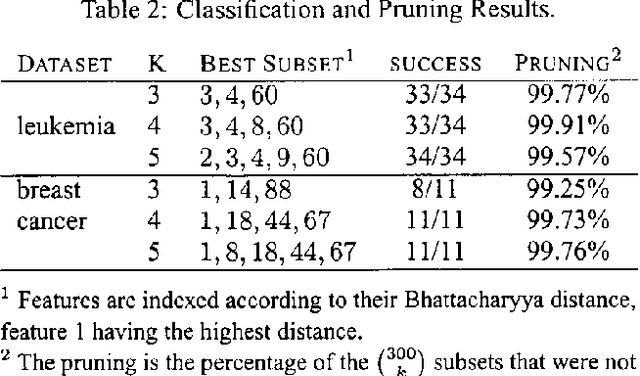
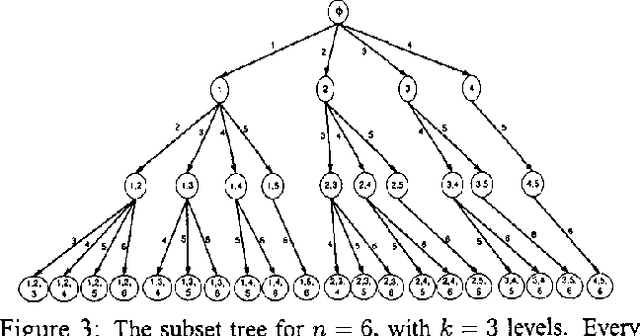
There is no known efficient method for selecting k Gaussian features from n which achieve the lowest Bayesian classification error. We show an example of how greedy algorithms faced with this task are led to give results that are not optimal. This motivates us to propose a more robust approach. We present a Branch and Bound algorithm for finding a subset of k independent Gaussian features which minimizes the naive Bayesian classification error. Our algorithm uses additive monotonic distance measures to produce bounds for the Bayesian classification error in order to exclude many feature subsets from evaluation, while still returning an optimal solution. We test our method on synthetic data as well as data obtained from gene expression profiling.