A Distance-Based Branch and Bound Feature Selection Algorithm
Paper and Code
Oct 19, 2012

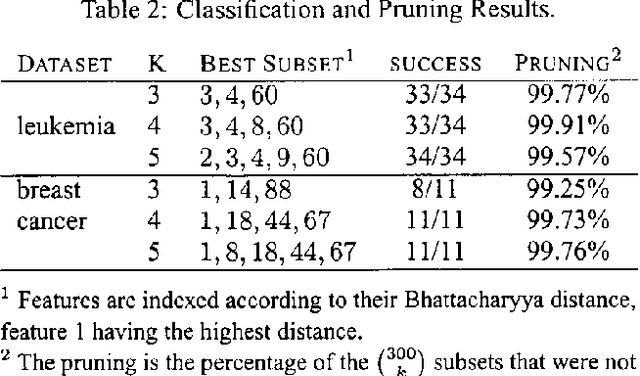
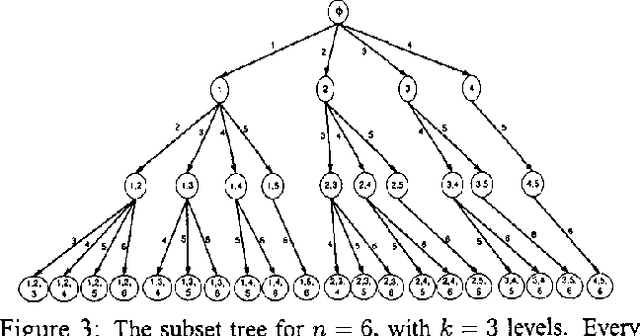
There is no known efficient method for selecting k Gaussian features from n which achieve the lowest Bayesian classification error. We show an example of how greedy algorithms faced with this task are led to give results that are not optimal. This motivates us to propose a more robust approach. We present a Branch and Bound algorithm for finding a subset of k independent Gaussian features which minimizes the naive Bayesian classification error. Our algorithm uses additive monotonic distance measures to produce bounds for the Bayesian classification error in order to exclude many feature subsets from evaluation, while still returning an optimal solution. We test our method on synthetic data as well as data obtained from gene expression profiling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge