Gradual Fine-Tuning with Graph Routing for Multi-Source Unsupervised Domain Adaptation

Multi-source unsupervised domain adaptation aims to leverage labeled data from multiple source domains for training a machine learning model to generalize well on a target domain without labels. Source domain selection plays a crucial role in determining the model's performance. It relies on the similarities amongst source and target domains. Nonetheless, existing work for source domain selection often involves heavyweight computational procedures, especially when dealing with numerous source domains and the need to identify the best ones from them. In this paper, we introduce a framework for gradual fine tuning (GFT) of machine learning models on multiple source domains. We represent multiple source domains as an undirected weighted graph. We then give a new generalization error bound for GFT along any path within the graph, which is used to determine the optimal path corresponding to the optimal training order. With this formulation, we introduce three lightweight graph-routing strategies which tend to minimize the error bound. Our best strategy improves $2.3\%$ of accuracy over the state-of-the-art on Natural Language Inference (NLI) task and achieves competitive performance on Sentiment Analysis (SA) task, especially a $3.9\%$ improvement on a more diverse subset of data we use for SA.

Learning Two-Layer Residual Networks with Nonparametric Function Estimation by Convex Programming

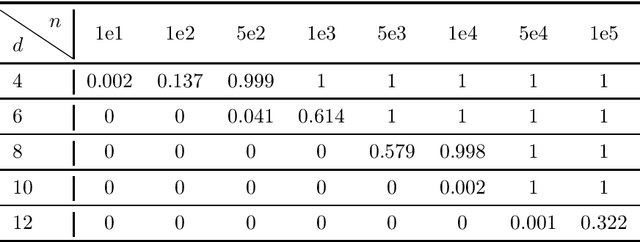
We focus on learning a two-layer residual neural network with preactivation by ReLU (preReLU-TLRN): Suppose the input $\mathbf{x}$ is from a distribution with support space $\mathbb{R}^d$ and the ground-truth generative model is a preReLU-TLRN, given by $$\mathbf{y} = \boldsymbol{B}^\ast\left[\left(\boldsymbol{A}^\ast\mathbf{x}\right)^+ + \mathbf{x}\right]\text{,}$$ where ground-truth network parameters $\boldsymbol{A}^\ast \in \mathbb{R}^{d\times d}$ is a nonnegative full-rank matrix and $\boldsymbol{B}^\ast \in \mathbb{R}^{m\times d}$ is full-rank with $m \geq d$. We design layerwise objectives as functionals whose analytic minimizers sufficiently express the exact ground-truth network in terms of its parameters and nonlinearities. Following this objective landscape, learning a preReLU-TLRN from finite samples can be formulated as convex programming with nonparametric function estimation: For each layer, we first formulate the corresponding empirical risk minimization (ERM) as convex quadratic programming (QP), then we show the solution space of the QP can be equivalently determined by a set of linear inequalities, which can then be efficiently solved by linear programming (LP). Experiments show the robustness and sample efficiency of our methods.

Image Deconvolution with Deep Image and Kernel Priors

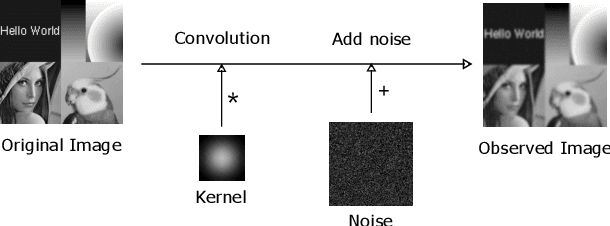
Image deconvolution is the process of recovering convolutional degraded images, which is always a hard inverse problem because of its mathematically ill-posed property. On the success of the recently proposed deep image prior (DIP), we build an image deconvolution model with deep image and kernel priors (DIKP). DIP is a learning-free representation which uses neural net structures to express image prior information, and it showed great success in many energy-based models, e.g. denoising, super-resolution, inpainting. Instead, our DIKP model uses such priors in image deconvolution to model not only images but also kernels, combining the ideas of traditional learning-free deconvolution methods with neural nets. In this paper, we show that DIKP improve the performance of learning-free image deconvolution, and we experimentally demonstrate this on the standard benchmark of six standard test images in terms of PSNR and visual effects.