Learning Two-Layer Residual Networks with Nonparametric Function Estimation by Convex Programming

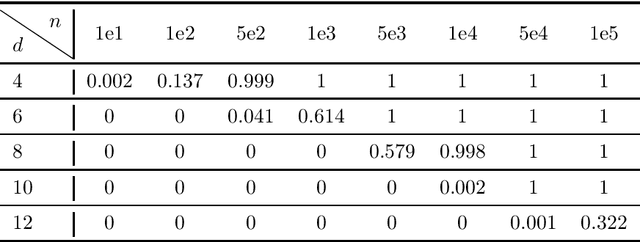
We focus on learning a two-layer residual neural network with preactivation by ReLU (preReLU-TLRN): Suppose the input $\mathbf{x}$ is from a distribution with support space $\mathbb{R}^d$ and the ground-truth generative model is a preReLU-TLRN, given by $$\mathbf{y} = \boldsymbol{B}^\ast\left[\left(\boldsymbol{A}^\ast\mathbf{x}\right)^+ + \mathbf{x}\right]\text{,}$$ where ground-truth network parameters $\boldsymbol{A}^\ast \in \mathbb{R}^{d\times d}$ is a nonnegative full-rank matrix and $\boldsymbol{B}^\ast \in \mathbb{R}^{m\times d}$ is full-rank with $m \geq d$. We design layerwise objectives as functionals whose analytic minimizers sufficiently express the exact ground-truth network in terms of its parameters and nonlinearities. Following this objective landscape, learning a preReLU-TLRN from finite samples can be formulated as convex programming with nonparametric function estimation: For each layer, we first formulate the corresponding empirical risk minimization (ERM) as convex quadratic programming (QP), then we show the solution space of the QP can be equivalently determined by a set of linear inequalities, which can then be efficiently solved by linear programming (LP). Experiments show the robustness and sample efficiency of our methods.