Respiration Monitoring of Multiple People using Multi-site FMCW SISO Radar Systems

Continuous contactless respiration monitoring of co-sleeping subjects faces a dilemma: conventional single-site multiple-input multiple-output (MIMO) radars struggle with limited angular resolution for closely spaced individuals, while distributed radar networks typically require complex hardware synchronization. To address these limitations, this paper proposes non-coherent multi-site single-input-single-output (SISO) radar systems that completely eliminate the need for physical synchronization cables or common reference clocks. The fundamental challenge of ghost target ambiguity in such non-coherent multilateration is resolved through a novel physiological-feature-assisted suppression technique. By exploiting the inherent statistical independence of individual respiratory rhythms, true target locations are robustly distinguished from ghosts via cross-correlation analysis. Experimental validation demonstrates that the proposed system can accurately resolve two subjects spaced less than 20 cm apart, surpassing the resolution limits of traditional compact MIMO arrays, while achieving a respiration rate estimation accuracy of 0.7 bpm root mean square error (RMSE) compared to contact-based ground truth.

On Efficient and Robust Metrics for RANSAC Hypotheses and 3D Rigid Registration

This paper focuses on developing efficient and robust evaluation metrics for RANSAC hypotheses to achieve accurate 3D rigid registration. Estimating six-degree-of-freedom (6-DoF) pose from feature correspondences remains a popular approach to 3D rigid registration, where random sample consensus (RANSAC) is a de-facto choice to this problem. However, existing metrics for RANSAC hypotheses are either time-consuming or sensitive to common nuisances, parameter variations, and different application scenarios, resulting in performance deterioration in overall registration accuracy and speed. We alleviate this problem by first analyzing the contributions of inliers and outliers, and then proposing several efficient and robust metrics with different designing motivations for RANSAC hypotheses. Comparative experiments on four standard datasets with different nuisances and application scenarios verify that the proposed metrics can significantly improve the registration performance and are more robust than several state-of-the-art competitors, making them good gifts to practical applications. This work also draws an interesting conclusion, i.e., not all inliers are equal while all outliers should be equal, which may shed new light on this research problem.

3D Correspondence Grouping with Compatibility Features

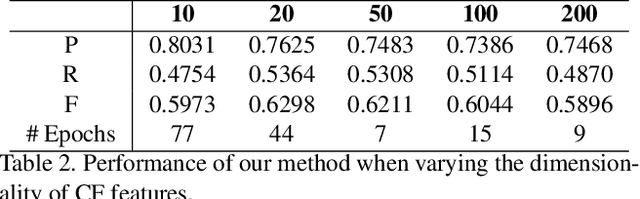
We present a simple yet effective method for 3D correspondence grouping. The objective is to accurately classify initial correspondences obtained by matching local geometric descriptors into inliers and outliers. Although the spatial distribution of correspondences is irregular, inliers are expected to be geometrically compatible with each other. Based on such observation, we propose a novel representation for 3D correspondences, dubbed compatibility feature (CF), to describe the consistencies within inliers and inconsistencies within outliers. CF consists of top-ranked compatibility scores of a candidate to other correspondences, which purely relies on robust and rotation-invariant geometric constraints. We then formulate the grouping problem as a classification problem for CF features, which is accomplished via a simple multilayer perceptron (MLP) network. Comparisons with nine state-of-the-art methods on four benchmarks demonstrate that: 1) CF is distinctive, robust, and rotation-invariant; 2) our CF-based method achieves the best overall performance and holds good generalization ability.