Scale-Distribution Decoupling: Enabling Stable and Effective Training of Large Language Models

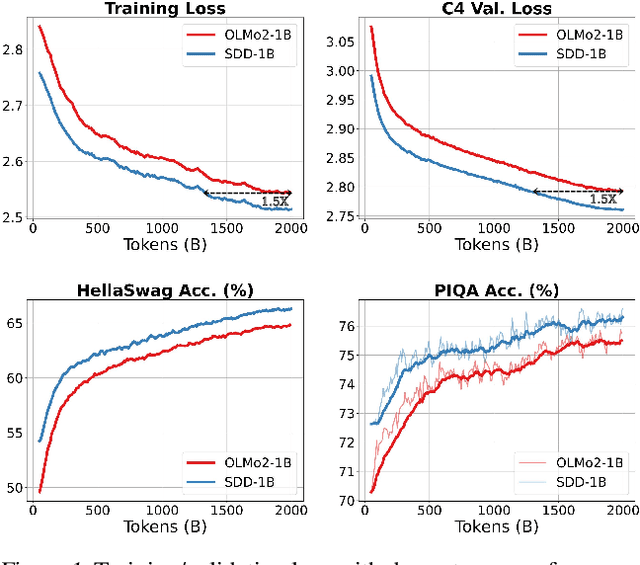
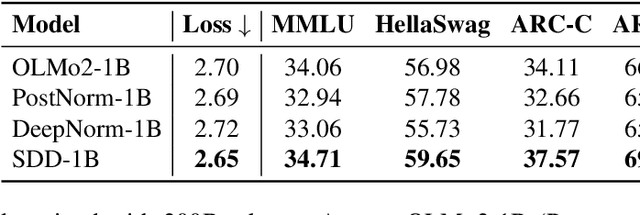
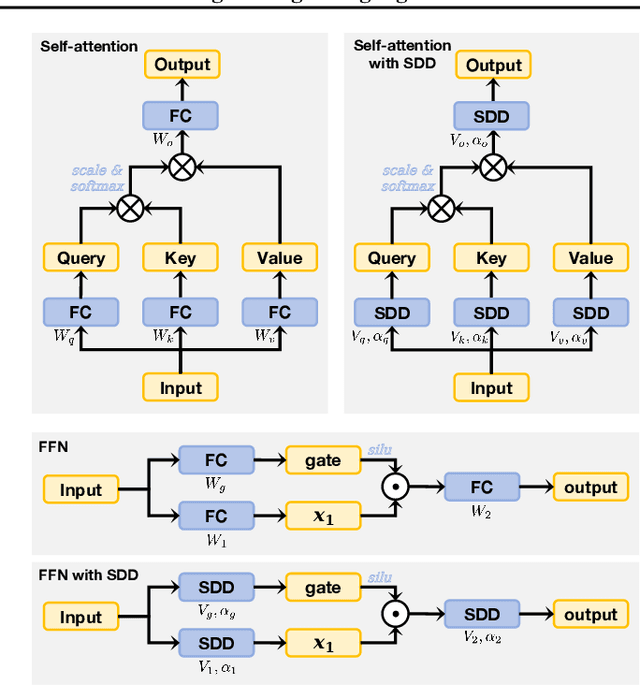
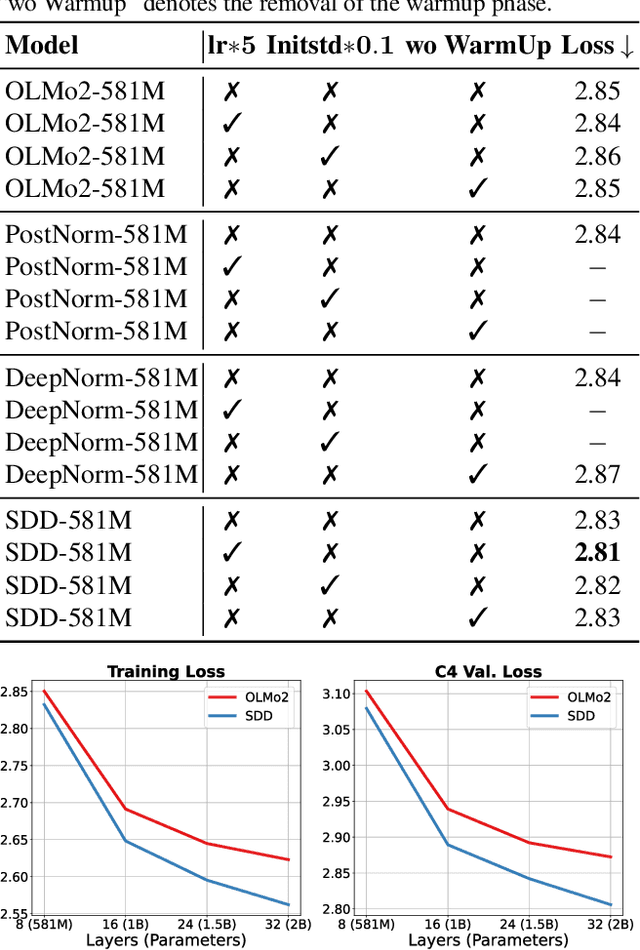
Training stability is a persistent challenge in the pre-training of large language models (LLMs), particularly for architectures such as Post-Norm Transformers, which are prone to gradient explosion and dissipation. In this paper, we propose Scale-Distribution Decoupling (SDD), a novel approach that stabilizes training by explicitly decoupling the scale and distribution of the weight matrix in fully-connected layers. SDD applies a normalization mechanism to regulate activations and a learnable scaling vector to maintain well-conditioned gradients, effectively preventing $\textbf{gradient explosion and dissipation}$. This separation improves optimization efficiency, particularly in deep networks, by ensuring stable gradient propagation. Experimental results demonstrate that our method stabilizes training across various LLM architectures and outperforms existing techniques in different normalization configurations. Furthermore, the proposed method is lightweight and compatible with existing frameworks, making it a practical solution for stabilizing LLM training. Code is available at https://github.com/kaihemo/SDD.

Polynomial Composition Activations: Unleashing the Dynamics of Large Language Models

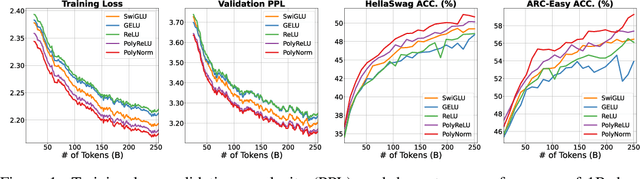
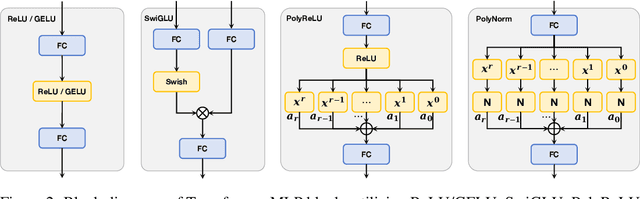
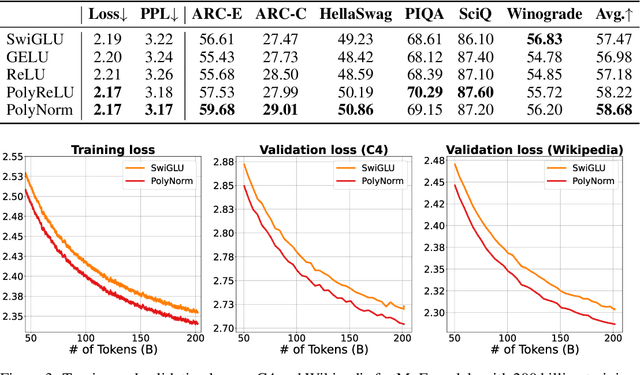
Transformers have found extensive applications across various domains due to the powerful fitting capabilities. This success can be partially attributed to their inherent nonlinearity. Thus, in addition to the ReLU function employed in the original transformer architecture, researchers have explored alternative modules such as GeLU and SwishGLU to enhance nonlinearity and thereby augment representational capacity. In this paper, we propose a novel category of polynomial composition activations (PolyCom), designed to optimize the dynamics of transformers. Theoretically, we provide a comprehensive mathematical analysis of PolyCom, highlighting its enhanced expressivity and efficacy relative to other activation functions. Notably, we demonstrate that networks incorporating PolyCom achieve the $\textbf{optimal approximation rate}$, indicating that PolyCom networks require minimal parameters to approximate general smooth functions in Sobolev spaces. We conduct empirical experiments on the pre-training configurations of large language models (LLMs), including both dense and sparse architectures. By substituting conventional activation functions with PolyCom, we enable LLMs to capture higher-order interactions within the data, thus improving performance metrics in terms of accuracy and convergence rates. Extensive experimental results demonstrate the effectiveness of our method, showing substantial improvements over other activation functions. Code is available at https://github.com/BryceZhuo/PolyCom.

Towards a Unified Theoretical Understanding of Non-contrastive Learning via Rank Differential Mechanism

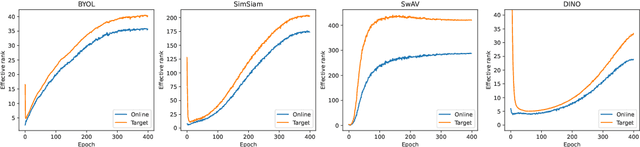
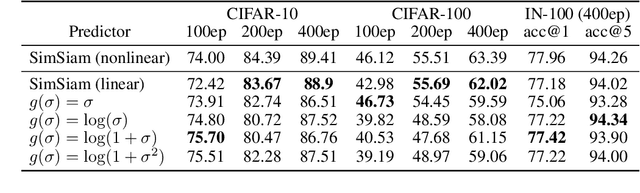
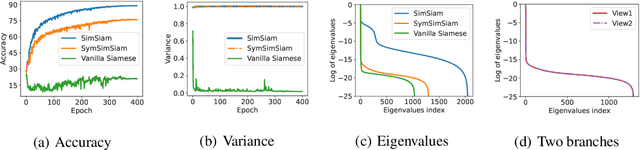
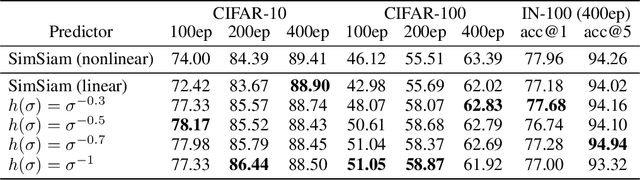
Recently, a variety of methods under the name of non-contrastive learning (like BYOL, SimSiam, SwAV, DINO) show that when equipped with some asymmetric architectural designs, aligning positive pairs alone is sufficient to attain good performance in self-supervised visual learning. Despite some understandings of some specific modules (like the predictor in BYOL), there is yet no unified theoretical understanding of how these seemingly different asymmetric designs can all avoid feature collapse, particularly considering methods that also work without the predictor (like DINO). In this work, we propose a unified theoretical understanding for existing variants of non-contrastive learning. Our theory named Rank Differential Mechanism (RDM) shows that all these asymmetric designs create a consistent rank difference in their dual-branch output features. This rank difference will provably lead to an improvement of effective dimensionality and alleviate either complete or dimensional feature collapse. Different from previous theories, our RDM theory is applicable to different asymmetric designs (with and without the predictor), and thus can serve as a unified understanding of existing non-contrastive learning methods. Besides, our RDM theory also provides practical guidelines for designing many new non-contrastive variants. We show that these variants indeed achieve comparable performance to existing methods on benchmark datasets, and some of them even outperform the baselines. Our code is available at \url{https://github.com/PKU-ML/Rank-Differential-Mechanism}.