Quaternion Generative Adversarial Neural Networks and Applications to Color Image Inpainting

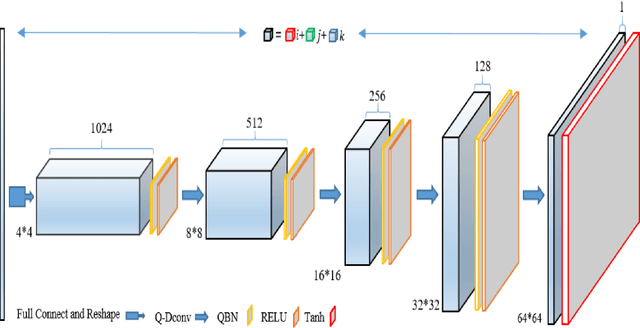
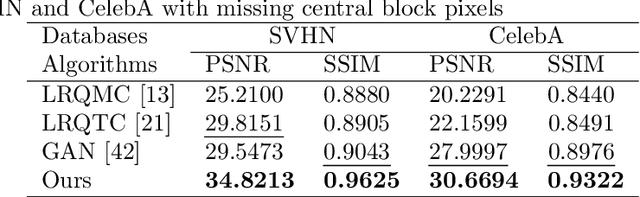
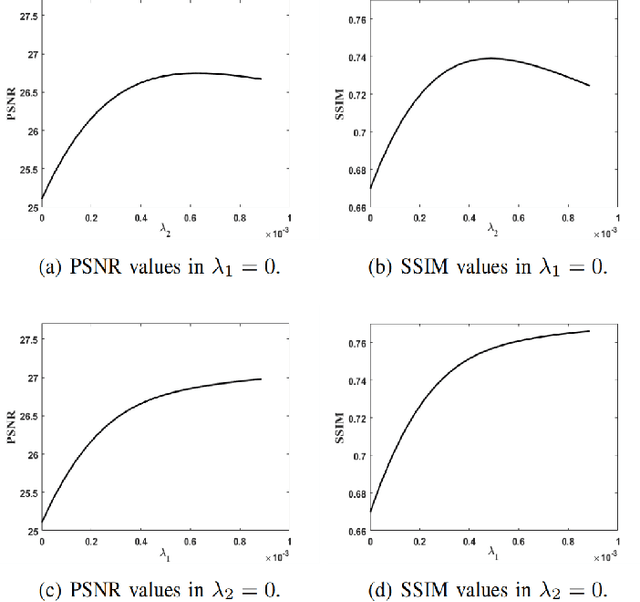
Color image inpainting is a challenging task in imaging science. The existing method is based on real operation, and the red, green and blue channels of the color image are processed separately, ignoring the correlation between each channel. In order to make full use of the correlation between each channel, this paper proposes a Quaternion Generative Adversarial Neural Network (QGAN) model and related theory, and applies it to solve the problem of color image inpainting with large area missing. Firstly, the definition of quaternion deconvolution is given and the quaternion batch normalization is proposed. Secondly, the above two innovative modules are applied to generate adversarial networks to improve stability. Finally, QGAN is applied to color image inpainting and compared with other state-of-the-art algorithms. The experimental results show that QGAN has superiority in color image inpainting with large area missing.

A New Cross-Space Total Variation Regularization Model for Color Image Restoration with Quaternion Blur Operator

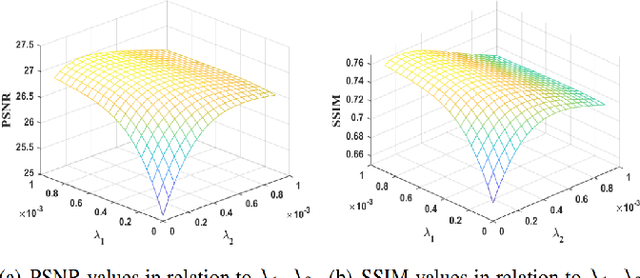
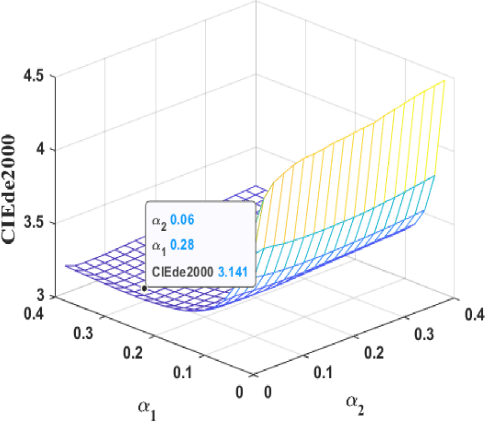
The cross-channel deblurring problem in color image processing is difficult to solve due to the complex coupling and structural blurring of color pixels. Until now, there are few efficient algorithms that can reduce color infection in deblurring process. To solve this challenging problem, we present a novel cross-space total variation (CSTV) regularization model for color image deblurring by introducing a quaternion blur operator and a cross-color space regularization functional. The existence and uniqueness of the solution is proved and a new L-curve method is proposed to find a sweet balance of regularization functionals on different color spaces. The Euler-Lagrange equation is derived to show that CSTV has taken into account the coupling of all color channels and the local smoothing within each color channel. A quaternion operator splitting method is firstly proposed to enhance the ability of color infection reduction of the CSTV regularization model. This strategy also applies to the well-known color deblurring models. Numerical experiments on color image databases illustrate the efficiency and manoeuvrability of the new model and algorithms. The color images restored by them successfully maintain the color and spatial information and are of higher quality in terms of PSNR, SSIM, MSE and CIEde2000 than the restorations of the-state-of-the-art methods.

A New Low-Rank Learning Robust Quaternion Tensor Completion Method for Color Video Inpainting Problem and Fast Algorithms

The color video inpainting problem is one of the most challenging problem in the modern imaging science. It aims to recover a color video from a small part of pixels that may contain noise. However, there are less of robust models that can simultaneously preserve the coupling of color channels and the evolution of color video frames. In this paper, we present a new robust quaternion tensor completion (RQTC) model to solve this challenging problem and derive the exact recovery theory. The main idea is to build a quaternion tensor optimization model to recover a low-rank quaternion tensor that represents the targeted color video and a sparse quaternion tensor that represents noise. This new model is very efficient to recover high dimensional data that satisfies the prior low-rank assumption. To solve the case without low-rank property, we introduce a new low-rank learning RQTC model, which rearranges similar patches classified by a quaternion learning method into smaller tensors satisfying the prior low-rank assumption. We also propose fast algorithms with global convergence guarantees. In numerical experiments, the proposed methods successfully recover color videos with eliminating color contamination and keeping the continuity of video scenery, and their solutions are of higher quality in terms of PSNR and SSIM values than the state-of-the-art algorithms.

Quasi Non-Negative Quaternion Matrix Factorization with Application to Color Face Recognition

To address the non-negativity dropout problem of quaternion models, a novel quasi non-negative quaternion matrix factorization (QNQMF) model is presented for color image processing. To implement QNQMF, the quaternion projected gradient algorithm and the quaternion alternating direction method of multipliers are proposed via formulating QNQMF as the non-convex constraint quaternion optimization problems. Some properties of the proposed algorithms are studied. The numerical experiments on the color image reconstruction show that these algorithms encoded on the quaternion perform better than these algorithms encoded on the red, green and blue channels. Furthermore, we apply the proposed algorithms to the color face recognition. Numerical results indicate that the accuracy rate of face recognition on the quaternion model is better than on the red, green and blue channels of color image as well as single channel of gray level images for the same data, when large facial expressions and shooting angle variations are presented.

Non-Local Robust Quaternion Matrix Completion for Large-Scale Color Images and Videos Inpainting

The image nonlocal self-similarity (NSS) prior refers to the fact that a local patch often has many nonlocal similar patches to it across the image. In this paper we apply such NSS prior to enhance the robust quaternion matrix completion (QMC) method and significantly improve the inpainting performance. A patch group based NSS prior learning scheme is proposed to learn explicit NSS models from natural color images. The NSS-based QMC algorithm computes an optimal low-rank approximation to the high-rank color image, resulting in high PSNR and SSIM measures and particularly the better visual quality. A new joint NSS-base QMC method is also presented to solve the color video inpainting problem based quaternion tensor representation. The numerical experiments on large-scale color images and videos indicate the advantages of NSS-based QMC over the state-of-the-art methods.

Advanced Variations of Two-Dimensional Principal Component Analysis for Face Recognition

The two-dimensional principal component analysis (2DPCA) has become one of the most powerful tools of artificial intelligent algorithms. In this paper, we review 2DPCA and its variations, and propose a general ridge regression model to extract features from both row and column directions. To enhance the generalization ability of extracted features, a novel relaxed 2DPCA (R2DPCA) is proposed with a new ridge regression model. R2DPCA generates a weighting vector with utilizing the label information, and maximizes a relaxed criterion with applying an optimal algorithm to get the essential features. The R2DPCA-based approaches for face recognition and image reconstruction are also proposed and the selected principle components are weighted to enhance the role of main components. Numerical experiments on well-known standard databases indicate that R2DPCA has high generalization ability and can achieve a higher recognition rate than the state-of-the-art methods, including in the deep learning methods such as CNNs, DBNs, and DNNs.

Sample-Relaxed Two-Dimensional Color Principal Component Analysis for Face Recognition and Image Reconstruction

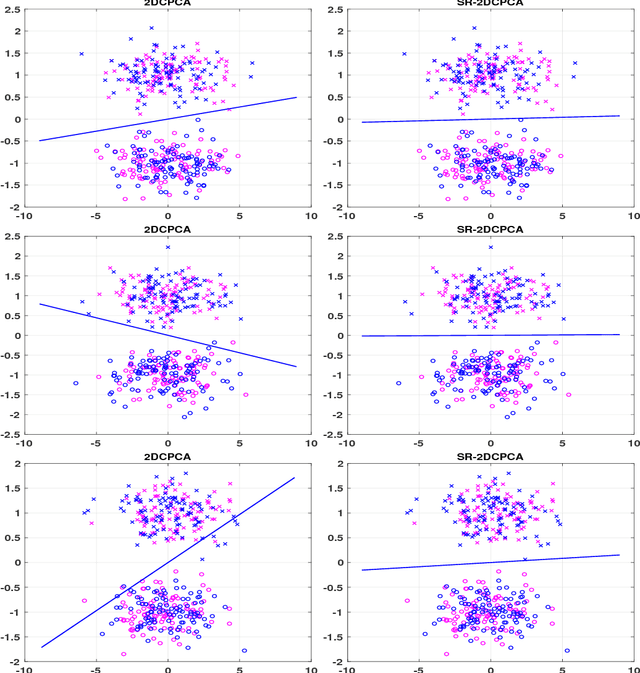
A sample-relaxed two-dimensional color principal component analysis (SR-2DCPCA) approach is presented for face recognition and image reconstruction based on quaternion models. A relaxation vector is automatically generated according to the variances of training color face images with the same label. A sample-relaxed, low-dimensional covariance matrix is constructed based on all the training samples relaxed by a relaxation vector, and its eigenvectors corresponding to the $r$ largest eigenvalues are defined as the optimal projection. The SR-2DCPCA aims to enlarge the global variance rather than to maximize the variance of the projected training samples. The numerical results based on real face data sets validate that SR-2DCPCA has a higher recognition rate than state-of-the-art methods and is efficient in image reconstruction.