PrivSGP-VR: Differentially Private Variance-Reduced Stochastic Gradient Push with Tight Utility Bounds

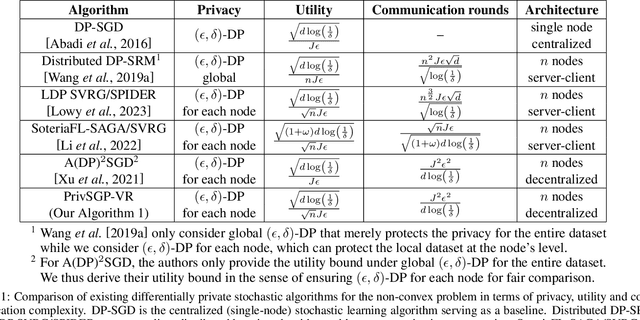
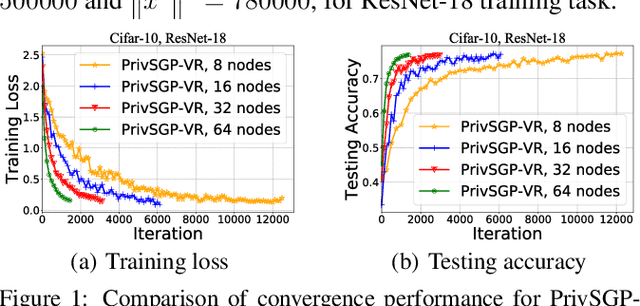
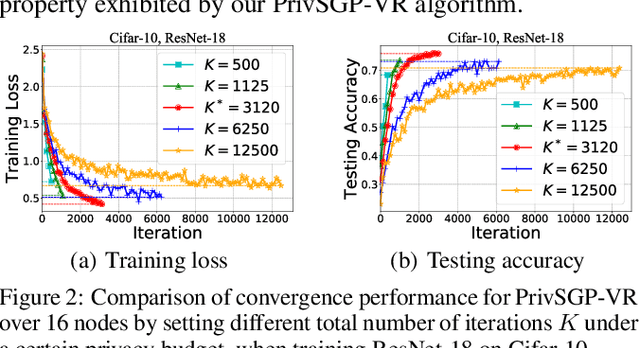
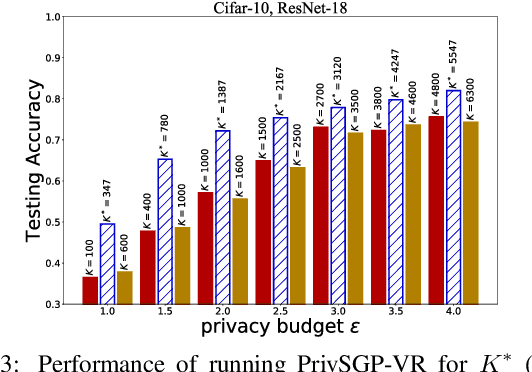
In this paper, we propose a differentially private decentralized learning method (termed PrivSGP-VR) which employs stochastic gradient push with variance reduction and guarantees $(\epsilon, \delta)$-differential privacy (DP) for each node. Our theoretical analysis shows that, under DP Gaussian noise with constant variance, PrivSGP-VR achieves a sub-linear convergence rate of $\mathcal{O}(1/\sqrt{nK})$, where $n$ and $K$ are the number of nodes and iterations, respectively, which is independent of stochastic gradient variance, and achieves a linear speedup with respect to $n$. Leveraging the moments accountant method, we further derive an optimal $K$ to maximize the model utility under certain privacy budget in decentralized settings. With this optimized $K$, PrivSGP-VR achieves a tight utility bound of $\mathcal{O}\left( \sqrt{d\log \left( \frac{1}{\delta} \right)}/(\sqrt{n}J\epsilon) \right)$, where $J$ and $d$ are the number of local samples and the dimension of decision variable, respectively, which matches that of the server-client distributed counterparts, and exhibits an extra factor of $1/\sqrt{n}$ improvement compared to that of the existing decentralized counterparts, such as A(DP)$^2$SGD. Extensive experiments corroborate our theoretical findings, especially in terms of the maximized utility with optimized $K$, in fully decentralized settings.

Robust Fully-Asynchronous Methods for Distributed Training over General Architecture

Perfect synchronization in distributed machine learning problems is inefficient and even impossible due to the existence of latency, package losses and stragglers. We propose a Robust Fully-Asynchronous Stochastic Gradient Tracking method (R-FAST), where each device performs local computation and communication at its own pace without any form of synchronization. Different from existing asynchronous distributed algorithms, R-FAST can eliminate the impact of data heterogeneity across devices and allow for packet losses by employing a robust gradient tracking strategy that relies on properly designed auxiliary variables for tracking and buffering the overall gradient vector. More importantly, the proposed method utilizes two spanning-tree graphs for communication so long as both share at least one common root, enabling flexible designs in communication architectures. We show that R-FAST converges in expectation to a neighborhood of the optimum with a geometric rate for smooth and strongly convex objectives; and to a stationary point with a sublinear rate for general non-convex settings. Extensive experiments demonstrate that R-FAST runs 1.5-2 times faster than synchronous benchmark algorithms, such as Ring-AllReduce and D-PSGD, while still achieving comparable accuracy, and outperforms existing asynchronous SOTA algorithms, such as AD-PSGD and OSGP, especially in the presence of stragglers.

Tackling Data Heterogeneity: A New Unified Framework for Decentralized SGD with Sample-induced Topology

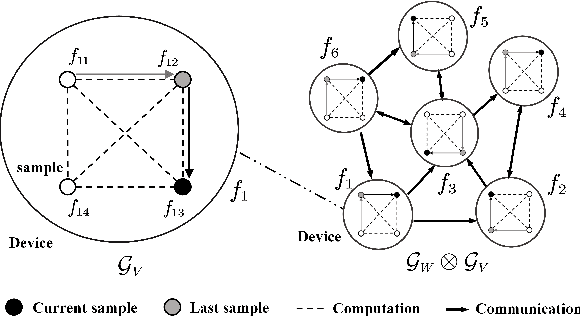
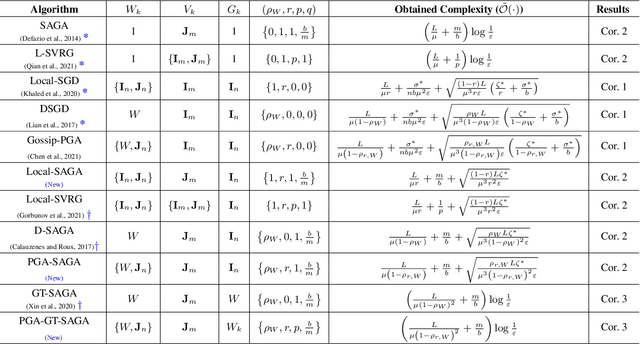
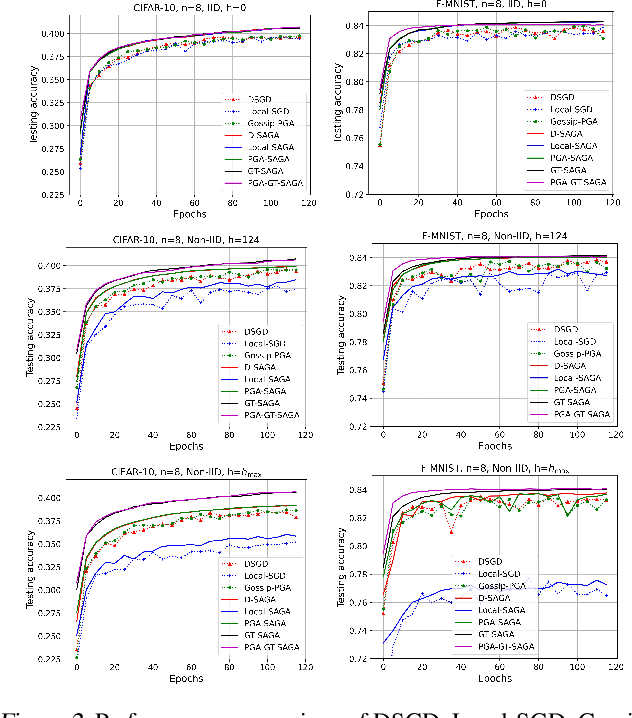
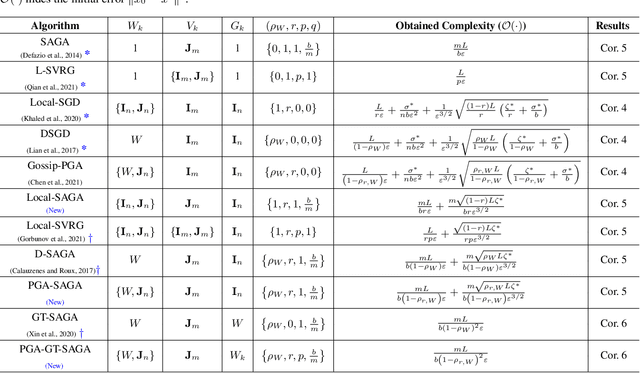
We develop a general framework unifying several gradient-based stochastic optimization methods for empirical risk minimization problems both in centralized and distributed scenarios. The framework hinges on the introduction of an augmented graph consisting of nodes modeling the samples and edges modeling both the inter-device communication and intra-device stochastic gradient computation. By designing properly the topology of the augmented graph, we are able to recover as special cases the renowned Local-SGD and DSGD algorithms, and provide a unified perspective for variance-reduction (VR) and gradient-tracking (GT) methods such as SAGA, Local-SVRG and GT-SAGA. We also provide a unified convergence analysis for smooth and (strongly) convex objectives relying on a proper structured Lyapunov function, and the obtained rate can recover the best known results for many existing algorithms. The rate results further reveal that VR and GT methods can effectively eliminate data heterogeneity within and across devices, respectively, enabling the exact convergence of the algorithm to the optimal solution. Numerical experiments confirm the findings in this paper.