PrivSGP-VR: Differentially Private Variance-Reduced Stochastic Gradient Push with Tight Utility Bounds

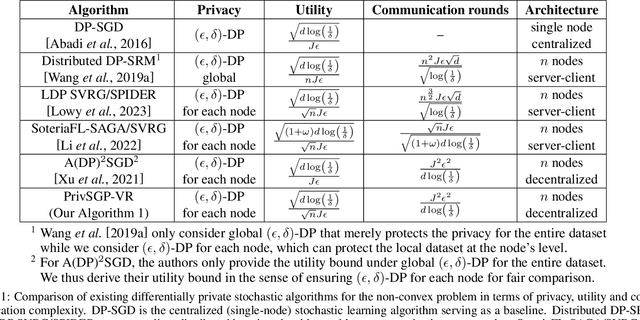
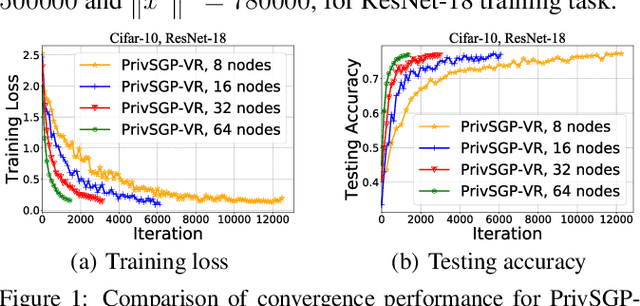
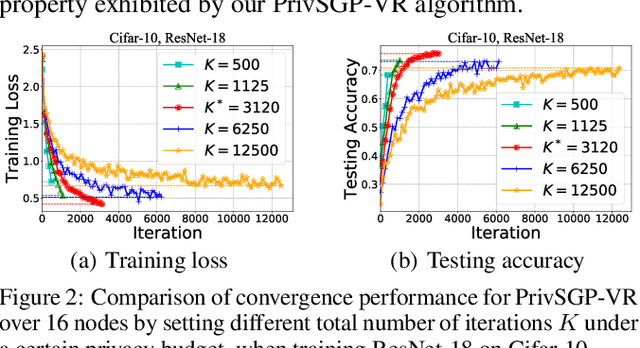
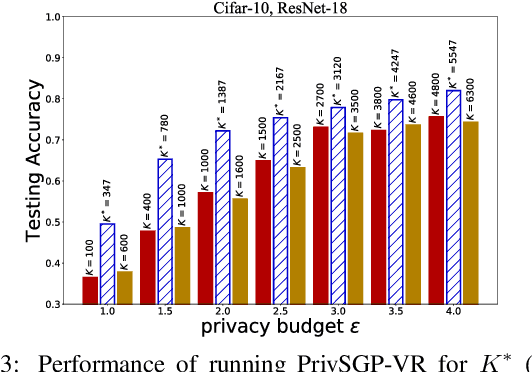
In this paper, we propose a differentially private decentralized learning method (termed PrivSGP-VR) which employs stochastic gradient push with variance reduction and guarantees $(\epsilon, \delta)$-differential privacy (DP) for each node. Our theoretical analysis shows that, under DP Gaussian noise with constant variance, PrivSGP-VR achieves a sub-linear convergence rate of $\mathcal{O}(1/\sqrt{nK})$, where $n$ and $K$ are the number of nodes and iterations, respectively, which is independent of stochastic gradient variance, and achieves a linear speedup with respect to $n$. Leveraging the moments accountant method, we further derive an optimal $K$ to maximize the model utility under certain privacy budget in decentralized settings. With this optimized $K$, PrivSGP-VR achieves a tight utility bound of $\mathcal{O}\left( \sqrt{d\log \left( \frac{1}{\delta} \right)}/(\sqrt{n}J\epsilon) \right)$, where $J$ and $d$ are the number of local samples and the dimension of decision variable, respectively, which matches that of the server-client distributed counterparts, and exhibits an extra factor of $1/\sqrt{n}$ improvement compared to that of the existing decentralized counterparts, such as A(DP)$^2$SGD. Extensive experiments corroborate our theoretical findings, especially in terms of the maximized utility with optimized $K$, in fully decentralized settings.