Yuxin Yao
Particulate: Feed-Forward 3D Object Articulation
Dec 12, 2025Abstract:We present Particulate, a feed-forward approach that, given a single static 3D mesh of an everyday object, directly infers all attributes of the underlying articulated structure, including its 3D parts, kinematic structure, and motion constraints. At its core is a transformer network, Part Articulation Transformer, which processes a point cloud of the input mesh using a flexible and scalable architecture to predict all the aforementioned attributes with native multi-joint support. We train the network end-to-end on a diverse collection of articulated 3D assets from public datasets. During inference, Particulate lifts the network's feed-forward prediction to the input mesh, yielding a fully articulated 3D model in seconds, much faster than prior approaches that require per-object optimization. Particulate can also accurately infer the articulated structure of AI-generated 3D assets, enabling full-fledged extraction of articulated 3D objects from a single (real or synthetic) image when combined with an off-the-shelf image-to-3D generator. We further introduce a new challenging benchmark for 3D articulation estimation curated from high-quality public 3D assets, and redesign the evaluation protocol to be more consistent with human preferences. Quantitative and qualitative results show that Particulate significantly outperforms state-of-the-art approaches.
DualReg: Dual-Space Filtering and Reinforcement for Rigid Registration
Aug 23, 2025Abstract:Rigid registration, aiming to estimate a rigid transformation to align source and target data, play a crucial role in applications such as SLAM and 3D reconstruction. However, noisy, partially overlapping data and the need for real-time processing pose major challenges for rigid registration. Considering that feature-based matching can handle large transformation differences but suffers from limited accuracy, while local geometry-based matching can achieve fine-grained local alignment but relies heavily on a good initial transformation, we propose a novel dual-space paradigm to fully leverage the strengths of both approaches. First, we introduce an efficient filtering mechanism that incorporates a computationally lightweight single-point RANSAC algorithm followed by a refinement module to eliminate unreliable feature-based correspondences. Subsequently, we treat filtered correspondences as anchor points, extract geometric proxies, and formulates an effective objective function with a tailored solver to estimate the transformation. Experiments verify our method's effectiveness, as shown by achieving up to a 32x CPU-time speedup over MAC on KITTI with comparable accuracy.
SmallGS: Gaussian Splatting-based Camera Pose Estimation for Small-Baseline Videos
Apr 22, 2025Abstract:Dynamic videos with small baseline motions are ubiquitous in daily life, especially on social media. However, these videos present a challenge to existing pose estimation frameworks due to ambiguous features, drift accumulation, and insufficient triangulation constraints. Gaussian splatting, which maintains an explicit representation for scenes, provides a reliable novel view rasterization when the viewpoint change is small. Inspired by this, we propose SmallGS, a camera pose estimation framework that is specifically designed for small-baseline videos. SmallGS optimizes sequential camera poses using Gaussian splatting, which reconstructs the scene from the first frame in each video segment to provide a stable reference for the rest. The temporal consistency of Gaussian splatting within limited viewpoint differences reduced the requirement of sufficient depth variations in traditional camera pose estimation. We further incorporate pretrained robust visual features, e.g. DINOv2, into Gaussian splatting, where high-dimensional feature map rendering enhances the robustness of camera pose estimation. By freezing the Gaussian splatting and optimizing camera viewpoints based on rasterized features, SmallGS effectively learns camera poses without requiring explicit feature correspondences or strong parallax motion. We verify the effectiveness of SmallGS in small-baseline videos in TUM-Dynamics sequences, which achieves impressive accuracy in camera pose estimation compared to MonST3R and DORID-SLAM for small-baseline videos in dynamic scenes. Our project page is at: https://yuxinyao620.github.io/SmallGS
RigGS: Rigging of 3D Gaussians for Modeling Articulated Objects in Videos
Mar 21, 2025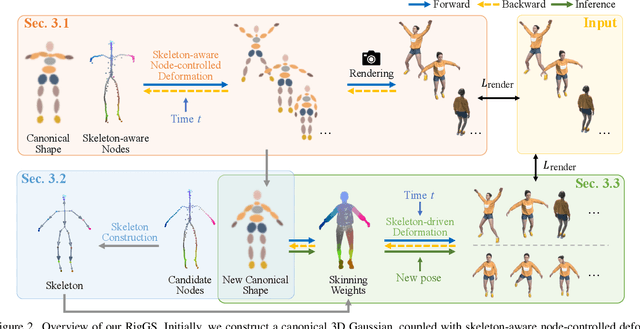
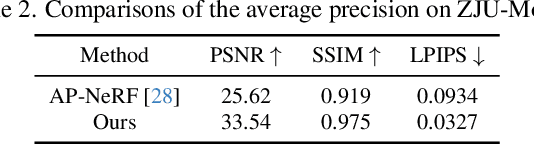
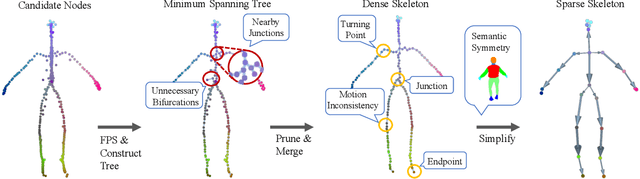

Abstract:This paper considers the problem of modeling articulated objects captured in 2D videos to enable novel view synthesis, while also being easily editable, drivable, and re-posable. To tackle this challenging problem, we propose RigGS, a new paradigm that leverages 3D Gaussian representation and skeleton-based motion representation to model dynamic objects without utilizing additional template priors. Specifically, we first propose skeleton-aware node-controlled deformation, which deforms a canonical 3D Gaussian representation over time to initialize the modeling process, producing candidate skeleton nodes that are further simplified into a sparse 3D skeleton according to their motion and semantic information. Subsequently, based on the resulting skeleton, we design learnable skin deformations and pose-dependent detailed deformations, thereby easily deforming the 3D Gaussian representation to generate new actions and render further high-quality images from novel views. Extensive experiments demonstrate that our method can generate realistic new actions easily for objects and achieve high-quality rendering.
SPARE: Symmetrized Point-to-Plane Distance for Robust Non-Rigid Registration
May 30, 2024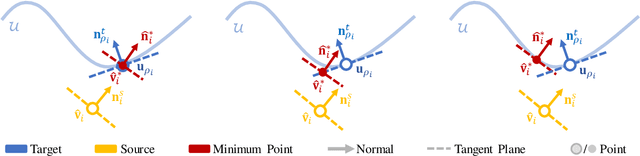
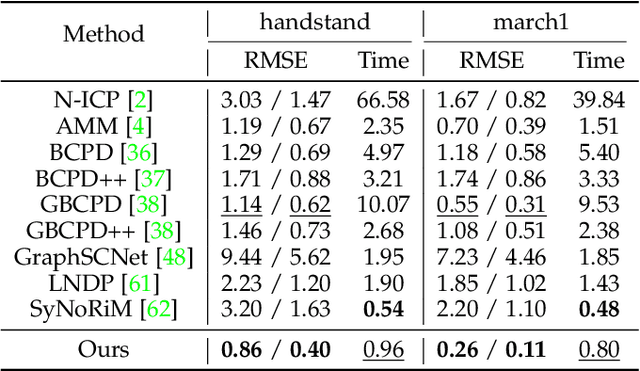
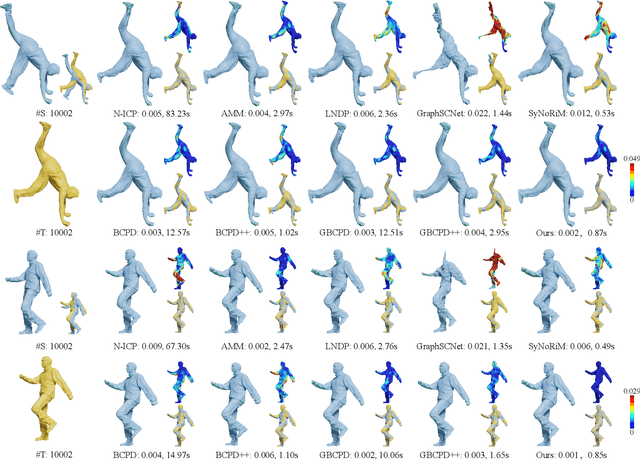
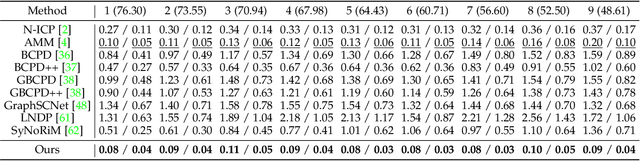
Abstract:Existing optimization-based methods for non-rigid registration typically minimize an alignment error metric based on the point-to-point or point-to-plane distance between corresponding point pairs on the source surface and target surface. However, these metrics can result in slow convergence or a loss of detail. In this paper, we propose SPARE, a novel formulation that utilizes a symmetrized point-to-plane distance for robust non-rigid registration. The symmetrized point-to-plane distance relies on both the positions and normals of the corresponding points, resulting in a more accurate approximation of the underlying geometry and can achieve higher accuracy than existing methods. To solve this optimization problem efficiently, we propose an alternating minimization solver using a majorization-minimization strategy. Moreover, for effective initialization of the solver, we incorporate a deformation graph-based coarse alignment that improves registration quality and efficiency. Extensive experiments show that the proposed method greatly improves the accuracy of non-rigid registration problems and maintains relatively high solution efficiency. The code is publicly available at https://github.com/yaoyx689/spare.
Neural-ABC: Neural Parametric Models for Articulated Body with Clothes
Apr 06, 2024Abstract:In this paper, we introduce Neural-ABC, a novel parametric model based on neural implicit functions that can represent clothed human bodies with disentangled latent spaces for identity, clothing, shape, and pose. Traditional mesh-based representations struggle to represent articulated bodies with clothes due to the diversity of human body shapes and clothing styles, as well as the complexity of poses. Our proposed model provides a unified framework for parametric modeling, which can represent the identity, clothing, shape and pose of the clothed human body. Our proposed approach utilizes the power of neural implicit functions as the underlying representation and integrates well-designed structures to meet the necessary requirements. Specifically, we represent the underlying body as a signed distance function and clothing as an unsigned distance function, and they can be uniformly represented as unsigned distance fields. Different types of clothing do not require predefined topological structures or classifications, and can follow changes in the underlying body to fit the body. Additionally, we construct poses using a controllable articulated structure. The model is trained on both open and newly constructed datasets, and our decoupling strategy is carefully designed to ensure optimal performance. Our model excels at disentangling clothing and identity in different shape and poses while preserving the style of the clothing. We demonstrate that Neural-ABC fits new observations of different types of clothing. Compared to other state-of-the-art parametric models, Neural-ABC demonstrates powerful advantages in the reconstruction of clothed human bodies, as evidenced by fitting raw scans, depth maps and images. We show that the attributes of the fitted results can be further edited by adjusting their identities, clothing, shape and pose codes.
DynoSurf: Neural Deformation-based Temporally Consistent Dynamic Surface Reconstruction
Mar 18, 2024



Abstract:This paper explores the problem of reconstructing temporally consistent surfaces from a 3D point cloud sequence without correspondence. To address this challenging task, we propose DynoSurf, an unsupervised learning framework integrating a template surface representation with a learnable deformation field. Specifically, we design a coarse-to-fine strategy for learning the template surface based on the deformable tetrahedron representation. Furthermore, we propose a learnable deformation representation based on the learnable control points and blending weights, which can deform the template surface non-rigidly while maintaining the consistency of the local shape. Experimental results demonstrate the significant superiority of DynoSurf over current state-of-the-art approaches, showcasing its potential as a powerful tool for dynamic mesh reconstruction. The code is publicly available at https://github.com/yaoyx689/DynoSurf.
Fast and Robust Non-Rigid Registration Using Accelerated Majorization-Minimization
Jun 08, 2022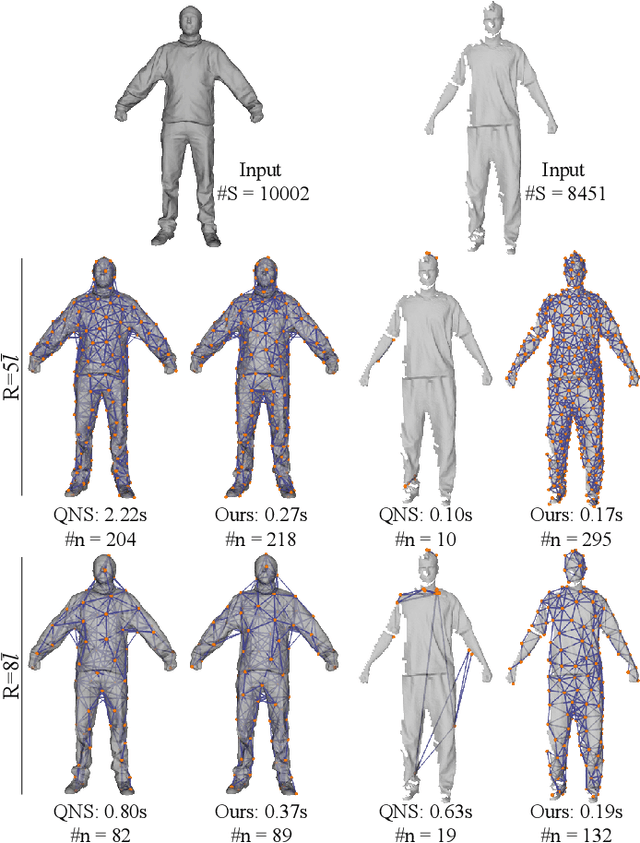
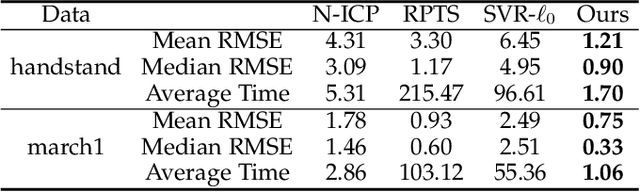
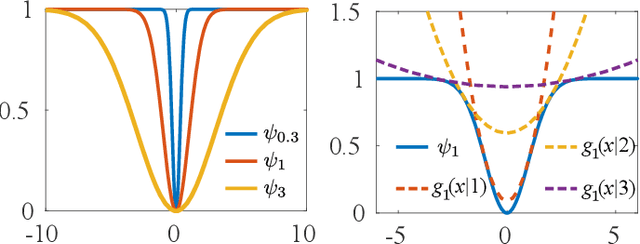
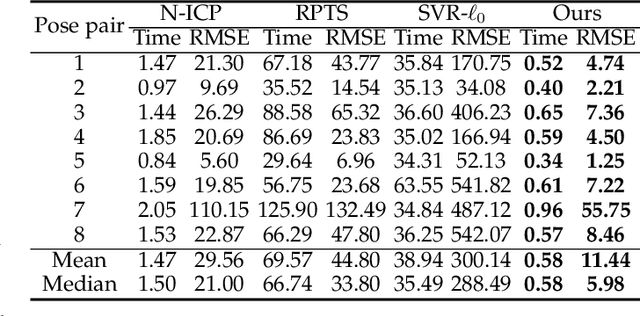
Abstract:Non-rigid registration, which deforms a source shape in a non-rigid way to align with a target shape, is a classical problem in computer vision. Such problems can be challenging because of imperfect data (noise, outliers and partial overlap) and high degrees of freedom. Existing methods typically adopt the $\ell_{p}$ type robust norm to measure the alignment error and regularize the smoothness of deformation, and use a proximal algorithm to solve the resulting non-smooth optimization problem. However, the slow convergence of such algorithms limits their wide applications. In this paper, we propose a formulation for robust non-rigid registration based on a globally smooth robust norm for alignment and regularization, which can effectively handle outliers and partial overlaps. The problem is solved using the majorization-minimization algorithm, which reduces each iteration to a convex quadratic problem with a closed-form solution. We further apply Anderson acceleration to speed up the convergence of the solver, enabling the solver to run efficiently on devices with limited compute capability. Extensive experiments demonstrate the effectiveness of our method for non-rigid alignment between two shapes with outliers and partial overlaps, with quantitative evaluation showing that it outperforms state-of-the-art methods in terms of registration accuracy and computational speed. The source code is available at https://github.com/yaoyx689/AMM_NRR.
A Survey of Non-Rigid 3D Registration
Mar 16, 2022



Abstract:Non-rigid registration computes an alignment between a source surface with a target surface in a non-rigid manner. In the past decade, with the advances in 3D sensing technologies that can measure time-varying surfaces, non-rigid registration has been applied for the acquisition of deformable shapes and has a wide range of applications. This survey presents a comprehensive review of non-rigid registration methods for 3D shapes, focusing on techniques related to dynamic shape acquisition and reconstruction. In particular, we review different approaches for representing the deformation field, and the methods for computing the desired deformation. Both optimization-based and learning-based methods are covered. We also review benchmarks and datasets for evaluating non-rigid registration methods, and discuss potential future research directions.
A Robust Loss for Point Cloud Registration
Aug 26, 2021
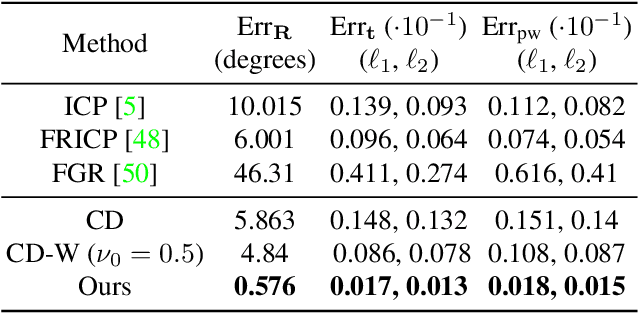
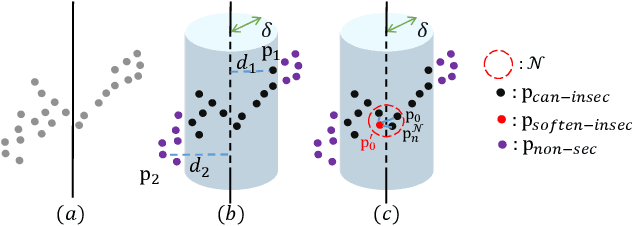
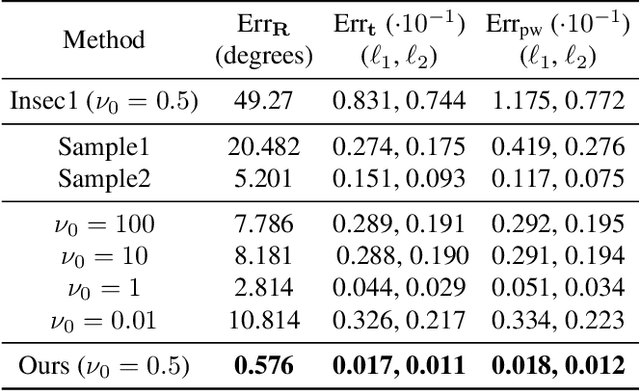
Abstract:The performance of surface registration relies heavily on the metric used for the alignment error between the source and target shapes. Traditionally, such a metric is based on the point-to-point or point-to-plane distance from the points on the source surface to their closest points on the target surface, which is susceptible to failure due to instability of the closest-point correspondence. In this paper, we propose a novel metric based on the intersection points between the two shapes and a random straight line, which does not assume a specific correspondence. We verify the effectiveness of this metric by extensive experiments, including its direct optimization for a single registration problem as well as unsupervised learning for a set of registration problems. The results demonstrate that the algorithms utilizing our proposed metric outperforms the state-of-the-art optimization-based and unsupervised learning-based methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge