Multi-Fidelity Bayesian Optimization With Across-Task Transferable Max-Value Entropy Search

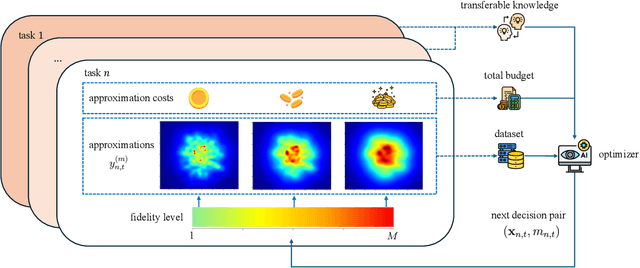
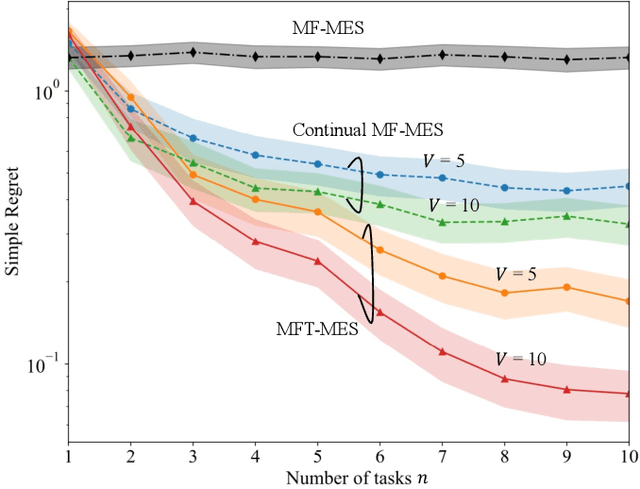
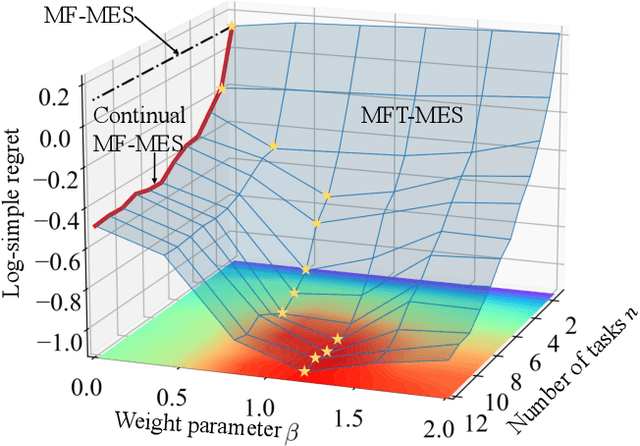
In many applications, ranging from logistics to engineering, a designer is faced with a sequence of optimization tasks for which the objectives are in the form of black-box functions that are costly to evaluate. For example, the designer may need to tune the hyperparameters of neural network models for different learning tasks over time. Rather than evaluating the objective function for each candidate solution, the designer may have access to approximations of the objective functions, for which higher-fidelity evaluations entail a larger cost. Existing multi-fidelity black-box optimization strategies select candidate solutions and fidelity levels with the goal of maximizing the information accrued about the optimal value or solution for the current task. Assuming that successive optimization tasks are related, this paper introduces a novel information-theoretic acquisition function that balances the need to acquire information about the current task with the goal of collecting information transferable to future tasks. The proposed method includes shared inter-task latent variables, which are transferred across tasks by implementing particle-based variational Bayesian updates. Experimental results across synthetic and real-world examples reveal that the proposed provident acquisition strategy that caters to future tasks can significantly improve the optimization efficiency as soon as a sufficient number of tasks is processed.

Bayesian Optimization with Formal Safety Guarantees via Online Conformal Prediction

Black-box zero-th order optimization is a central primitive for applications in fields as diverse as finance, physics, and engineering. In a common formulation of this problem, a designer sequentially attempts candidate solutions, receiving noisy feedback on the value of each attempt from the system. In this paper, we study scenarios in which feedback is also provided on the safety of the attempted solution, and the optimizer is constrained to limit the number of unsafe solutions that are tried throughout the optimization process. Focusing on methods based on Bayesian optimization (BO), prior art has introduced an optimization scheme -- referred to as SAFEOPT -- that is guaranteed not to select any unsafe solution with a controllable probability over feedback noise as long as strict assumptions on the safety constraint function are met. In this paper, a novel BO-based approach is introduced that satisfies safety requirements irrespective of properties of the constraint function. This strong theoretical guarantee is obtained at the cost of allowing for an arbitrary, controllable but non-zero, rate of violation of the safety constraint. The proposed method, referred to as SAFE-BOCP, builds on online conformal prediction (CP) and is specialized to the cases in which feedback on the safety constraint is either noiseless or noisy. Experimental results on synthetic and real-world data validate the advantages and flexibility of the proposed SAFE-BOCP.

Bayesian and Multi-Armed Contextual Meta-Optimization for Efficient Wireless Radio Resource Management

Optimal resource allocation in modern communication networks calls for the optimization of objective functions that are only accessible via costly separate evaluations for each candidate solution. The conventional approach carries out the optimization of resource-allocation parameters for each system configuration, characterized, e.g., by topology and traffic statistics, using global search methods such as Bayesian optimization (BO). These methods tend to require a large number of iterations, and hence a large number of key performance indicator (KPI) evaluations. In this paper, we propose the use of meta-learning to transfer knowledge from data collected from related, but distinct, configurations in order to speed up optimization on new network configurations. Specifically, we combine meta-learning with BO, as well as with multi-armed bandit (MAB) optimization, with the latter having the potential advantage of operating directly on a discrete search space. Furthermore, we introduce novel contextual meta-BO and meta-MAB algorithms, in which transfer of knowledge across configurations occurs at the level of a mapping from graph-based contextual information to resource-allocation parameters. Experiments for the problem of open loop power control (OLPC) parameter optimization for the uplink of multi-cell multi-antenna systems provide insights into the potential benefits of meta-learning and contextual optimization.

Leveraging Channel Noise for Sampling and Privacy via Quantized Federated Langevin Monte Carlo

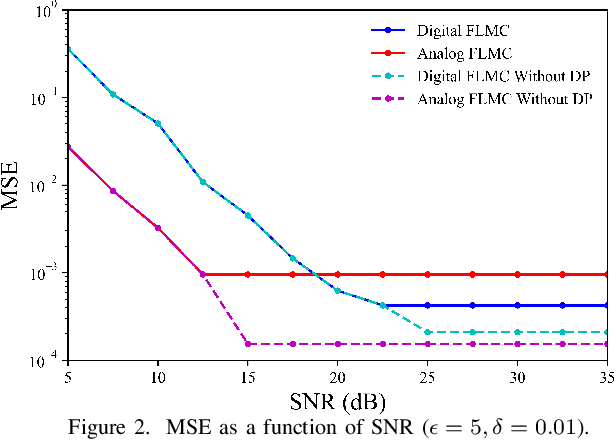
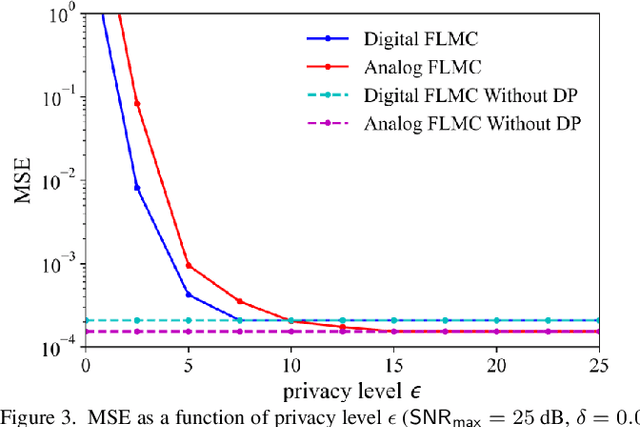
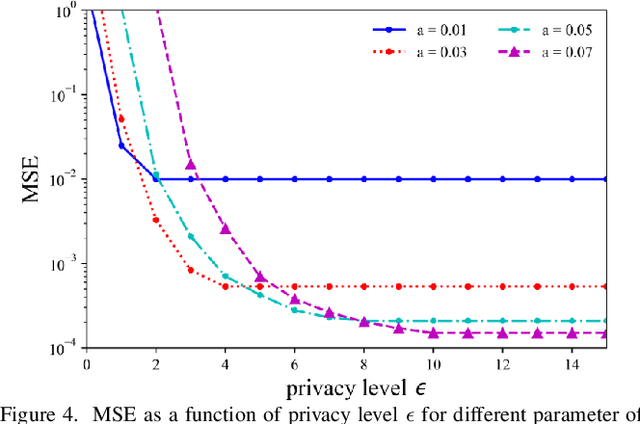
For engineering applications of artificial intelligence, Bayesian learning holds significant advantages over standard frequentist learning, including the capacity to quantify uncertainty. Langevin Monte Carlo (LMC) is an efficient gradient-based approximate Bayesian learning strategy that aims at producing samples drawn from the posterior distribution of the model parameters. Prior work focused on a distributed implementation of LMC over a multi-access wireless channel via analog modulation. In contrast, this paper proposes quantized federated LMC (FLMC), which integrates one-bit stochastic quantization of the local gradients with channel-driven sampling. Channel-driven sampling leverages channel noise for the purpose of contributing to Monte Carlo sampling, while also serving the role of privacy mechanism. Analog and digital implementations of wireless LMC are compared as a function of differential privacy (DP) requirements, revealing the advantages of the latter at sufficiently high signal-to-noise ratio.

Transfer Bayesian Meta-learning via Weighted Free Energy Minimization

Meta-learning optimizes the hyperparameters of a training procedure, such as its initialization, kernel, or learning rate, based on data sampled from a number of auxiliary tasks. A key underlying assumption is that the auxiliary tasks, known as meta-training tasks, share the same generating distribution as the tasks to be encountered at deployment time, known as meta-test tasks. This may, however, not be the case when the test environment differ from the meta-training conditions. To address shifts in task generating distribution between meta-training and meta-testing phases, this paper introduces weighted free energy minimization (WFEM) for transfer meta-learning. We instantiate the proposed approach for non-parametric Bayesian regression and classification via Gaussian Processes (GPs). The method is validated on a toy sinusoidal regression problem, as well as on classification using miniImagenet and CUB data sets, through comparison with standard meta-learning of GP priors as implemented by PACOH.