Leveraging Channel Noise for Sampling and Privacy via Quantized Federated Langevin Monte Carlo
Paper and Code
Feb 28, 2022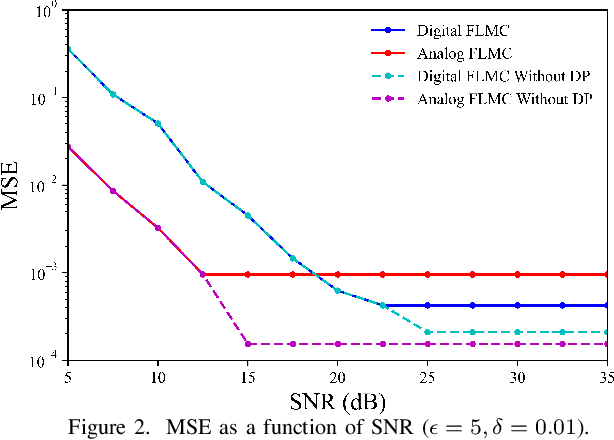
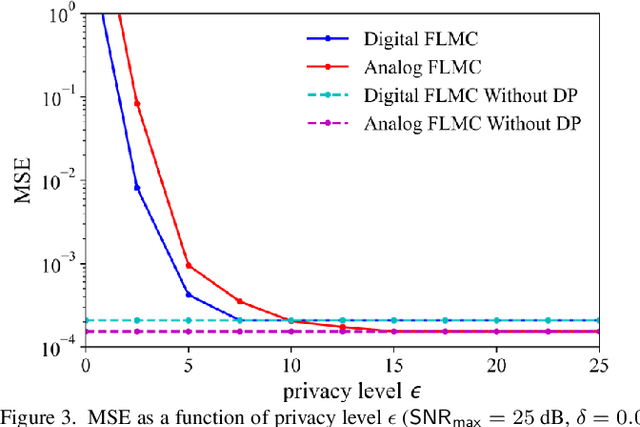
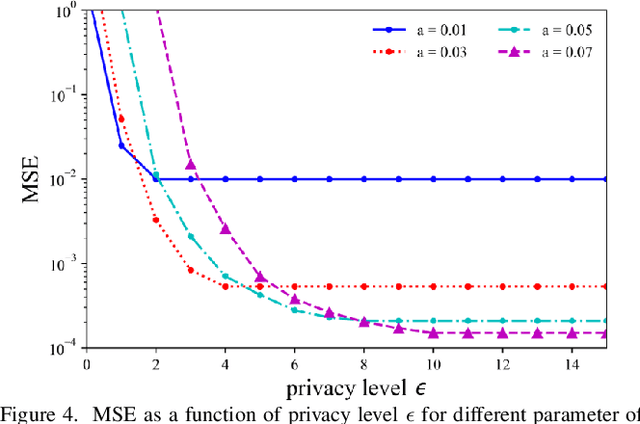
For engineering applications of artificial intelligence, Bayesian learning holds significant advantages over standard frequentist learning, including the capacity to quantify uncertainty. Langevin Monte Carlo (LMC) is an efficient gradient-based approximate Bayesian learning strategy that aims at producing samples drawn from the posterior distribution of the model parameters. Prior work focused on a distributed implementation of LMC over a multi-access wireless channel via analog modulation. In contrast, this paper proposes quantized federated LMC (FLMC), which integrates one-bit stochastic quantization of the local gradients with channel-driven sampling. Channel-driven sampling leverages channel noise for the purpose of contributing to Monte Carlo sampling, while also serving the role of privacy mechanism. Analog and digital implementations of wireless LMC are compared as a function of differential privacy (DP) requirements, revealing the advantages of the latter at sufficiently high signal-to-noise ratio.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge