Multi-Fidelity Bayesian Optimization With Across-Task Transferable Max-Value Entropy Search
Paper and Code
Mar 14, 2024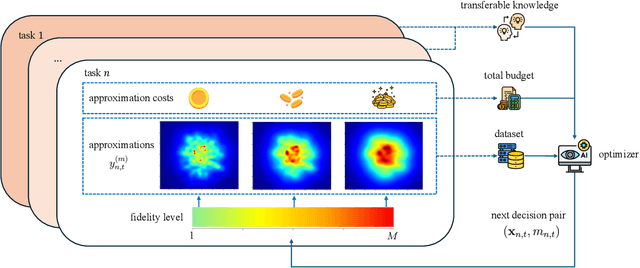
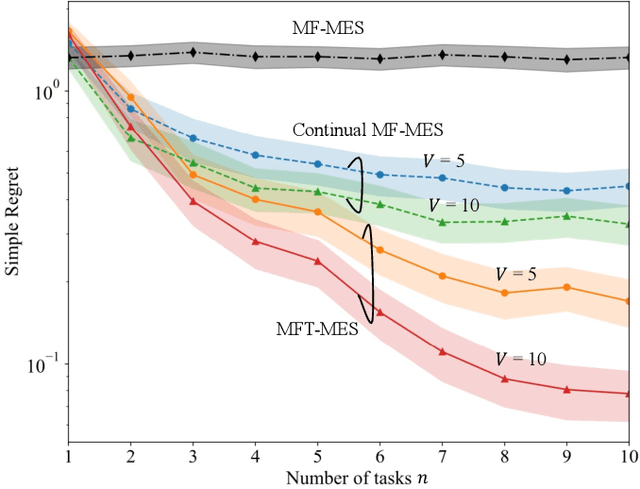
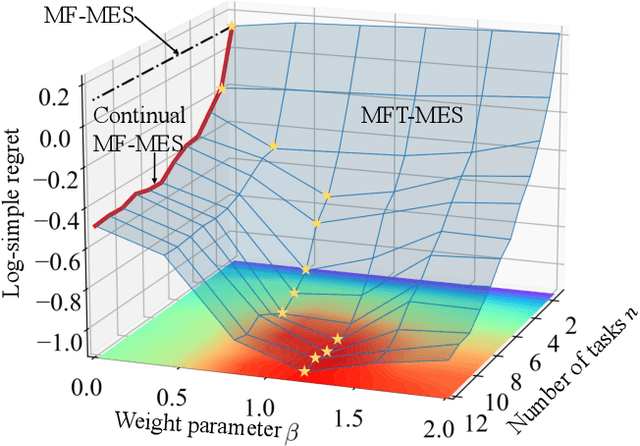
In many applications, ranging from logistics to engineering, a designer is faced with a sequence of optimization tasks for which the objectives are in the form of black-box functions that are costly to evaluate. For example, the designer may need to tune the hyperparameters of neural network models for different learning tasks over time. Rather than evaluating the objective function for each candidate solution, the designer may have access to approximations of the objective functions, for which higher-fidelity evaluations entail a larger cost. Existing multi-fidelity black-box optimization strategies select candidate solutions and fidelity levels with the goal of maximizing the information accrued about the optimal value or solution for the current task. Assuming that successive optimization tasks are related, this paper introduces a novel information-theoretic acquisition function that balances the need to acquire information about the current task with the goal of collecting information transferable to future tasks. The proposed method includes shared inter-task latent variables, which are transferred across tasks by implementing particle-based variational Bayesian updates. Experimental results across synthetic and real-world examples reveal that the proposed provident acquisition strategy that caters to future tasks can significantly improve the optimization efficiency as soon as a sufficient number of tasks is processed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge