Classes are not Clusters: Improving Label-based Evaluation of Dimensionality Reduction

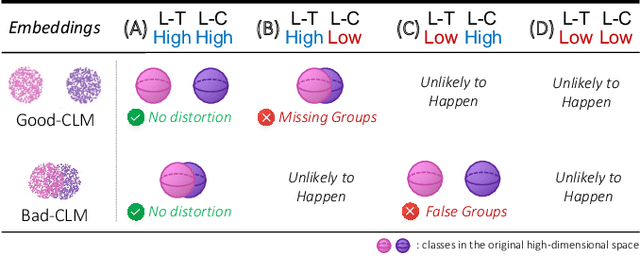
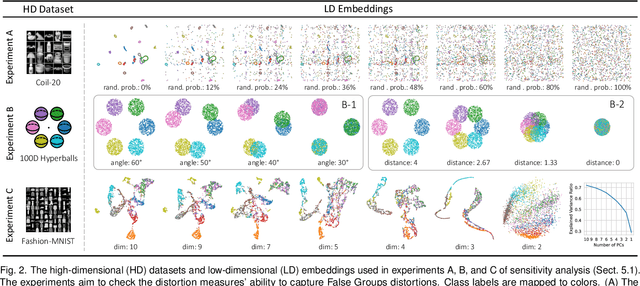
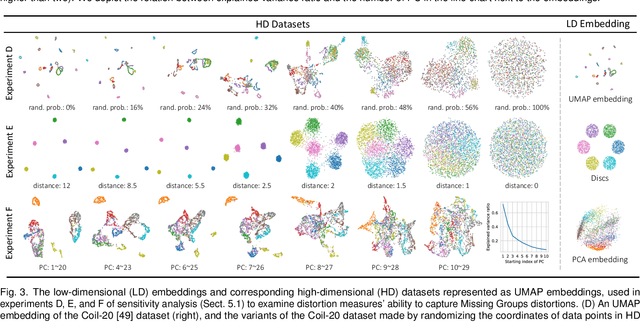
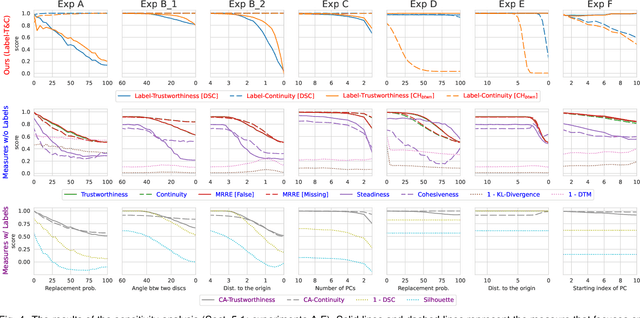
A common way to evaluate the reliability of dimensionality reduction (DR) embeddings is to quantify how well labeled classes form compact, mutually separated clusters in the embeddings. This approach is based on the assumption that the classes stay as clear clusters in the original high-dimensional space. However, in reality, this assumption can be violated; a single class can be fragmented into multiple separated clusters, and multiple classes can be merged into a single cluster. We thus cannot always assure the credibility of the evaluation using class labels. In this paper, we introduce two novel quality measures -- Label-Trustworthiness and Label-Continuity (Label-T&C) -- advancing the process of DR evaluation based on class labels. Instead of assuming that classes are well-clustered in the original space, Label-T&C work by (1) estimating the extent to which classes form clusters in the original and embedded spaces and (2) evaluating the difference between the two. A quantitative evaluation showed that Label-T&C outperform widely used DR evaluation measures (e.g., Trustworthiness and Continuity, Kullback-Leibler divergence) in terms of the accuracy in assessing how well DR embeddings preserve the cluster structure, and are also scalable. Moreover, we present case studies demonstrating that Label-T&C can be successfully used for revealing the intrinsic characteristics of DR techniques and their hyperparameters.

Feature Learning for Dimensionality Reduction toward Maximal Extraction of Hidden Patterns

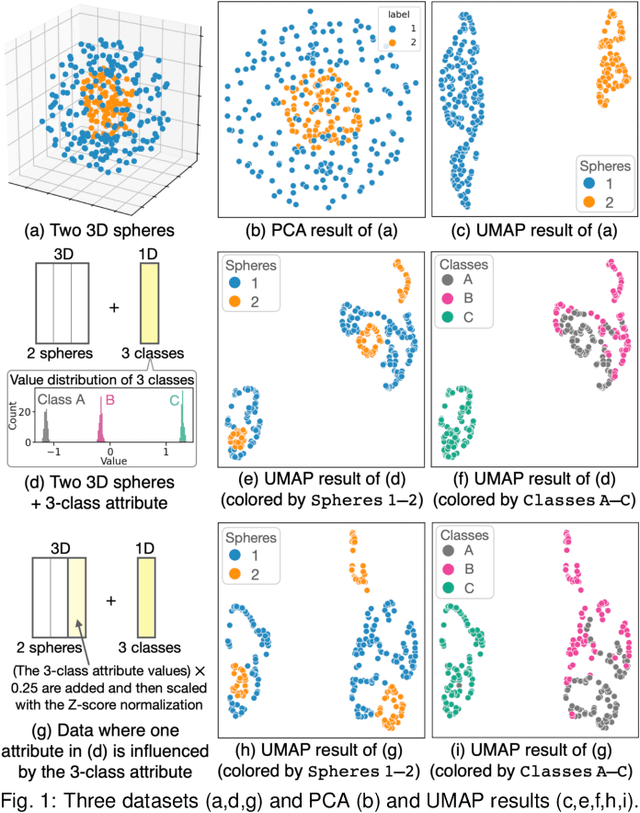
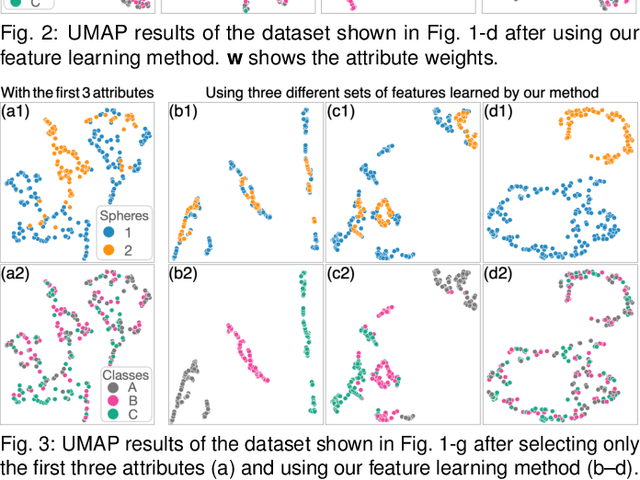
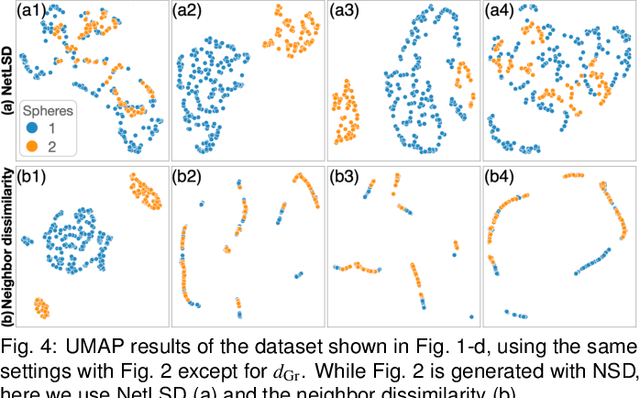
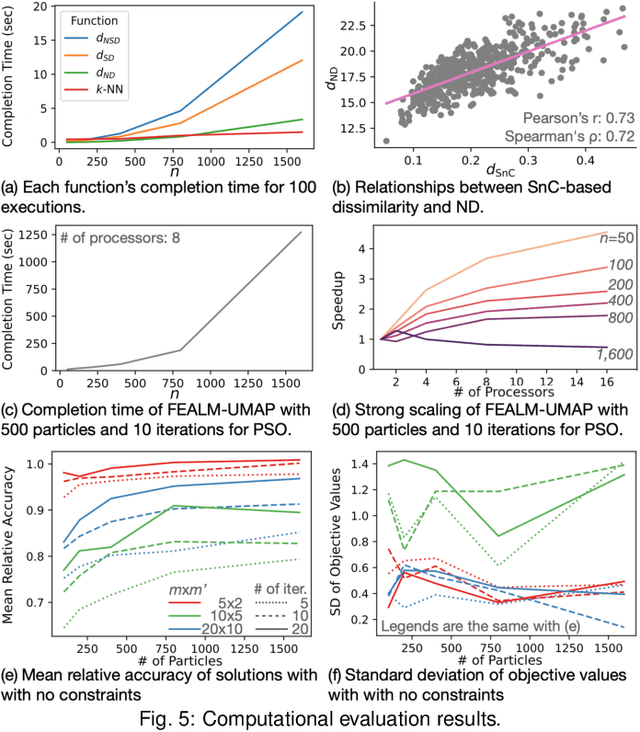
Dimensionality reduction (DR) plays a vital role in the visual analysis of high-dimensional data. One main aim of DR is to reveal hidden patterns that lie on intrinsic low-dimensional manifolds. However, DR often overlooks important patterns when the manifolds are strongly distorted or hidden by certain influential data attributes. This paper presents a feature learning framework, FEALM, designed to generate an optimized set of data projections for nonlinear DR in order to capture important patterns in the hidden manifolds. These projections produce maximally different nearest-neighbor graphs so that resultant DR outcomes are significantly different. To achieve such a capability, we design an optimization algorithm as well as introduce a new graph dissimilarity measure, called neighbor-shape dissimilarity. Additionally, we develop interactive visualizations to assist comparison of obtained DR results and interpretation of each DR result. We demonstrate FEALM's effectiveness through experiments using synthetic datasets and multiple case studies on real-world datasets.

A Machine-Learning-Aided Visual Analysis Workflow for Investigating Air Pollution Data

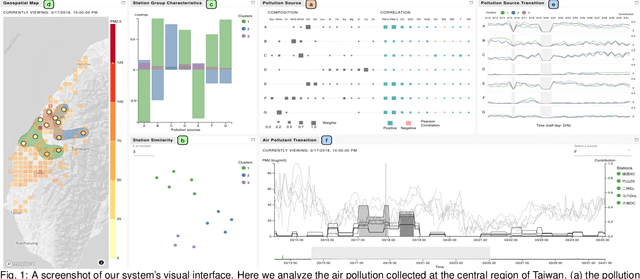
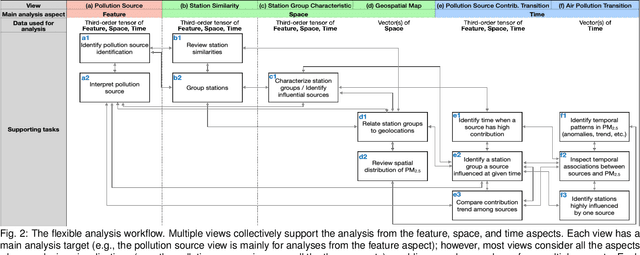
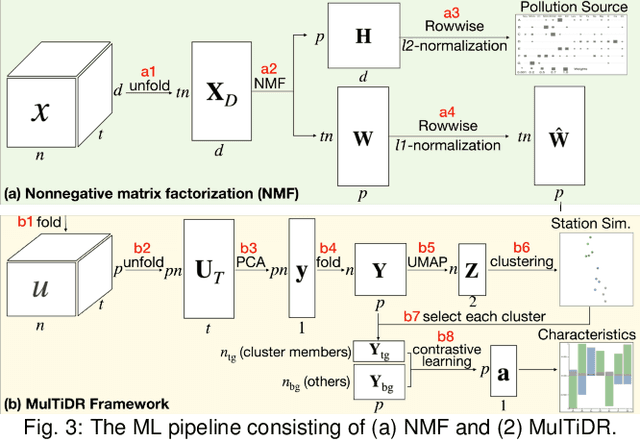
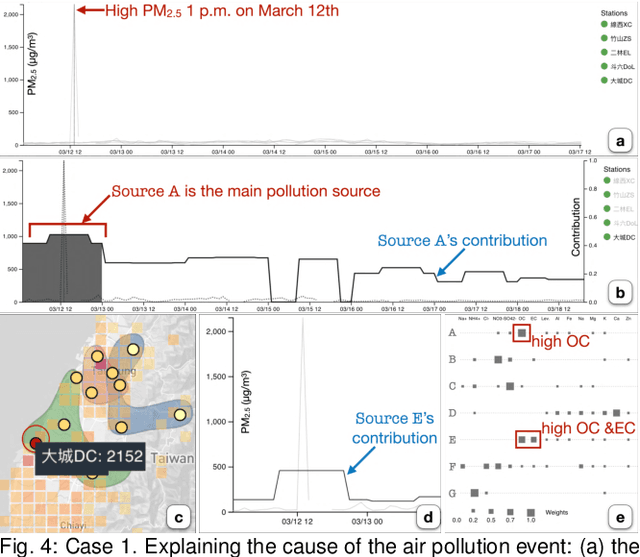
Analyzing air pollution data is challenging as there are various analysis focuses from different aspects: feature (what), space (where), and time (when). As in most geospatial analysis problems, besides high-dimensional features, the temporal and spatial dependencies of air pollution induce the complexity of performing analysis. Machine learning methods, such as dimensionality reduction, can extract and summarize important information of the data to lift the burden of understanding such a complicated environment. In this paper, we present a methodology that utilizes multiple machine learning methods to uniformly explore these aspects. With this methodology, we develop a visual analytic system that supports a flexible analysis workflow, allowing domain experts to freely explore different aspects based on their analysis needs. We demonstrate the capability of our system and analysis workflow supporting a variety of analysis tasks with multiple use cases.