Feature Learning for Dimensionality Reduction toward Maximal Extraction of Hidden Patterns
Paper and Code
Jun 28, 2022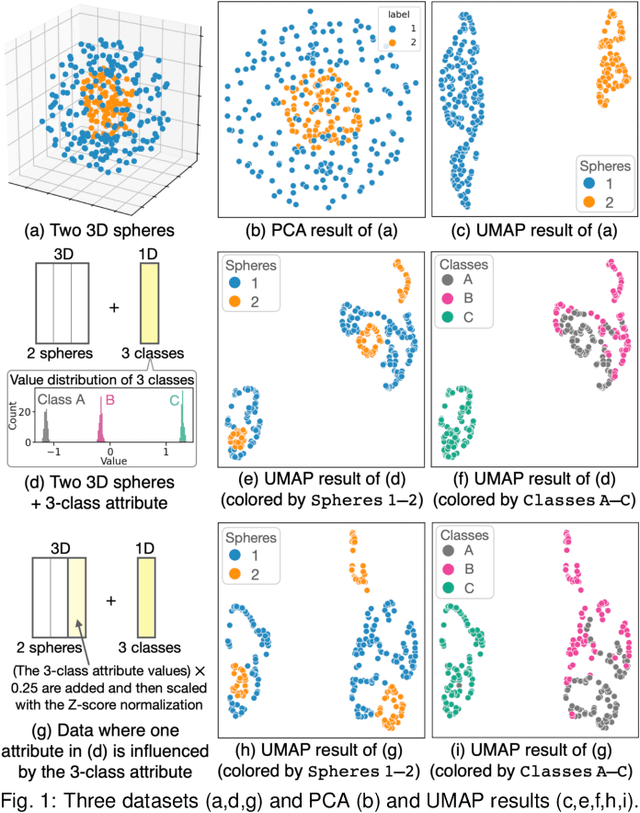
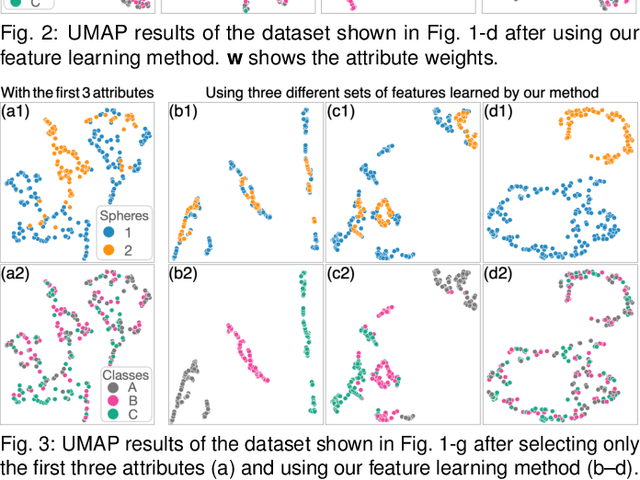
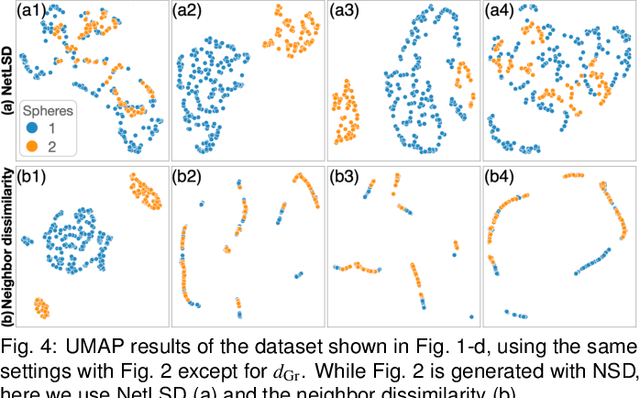
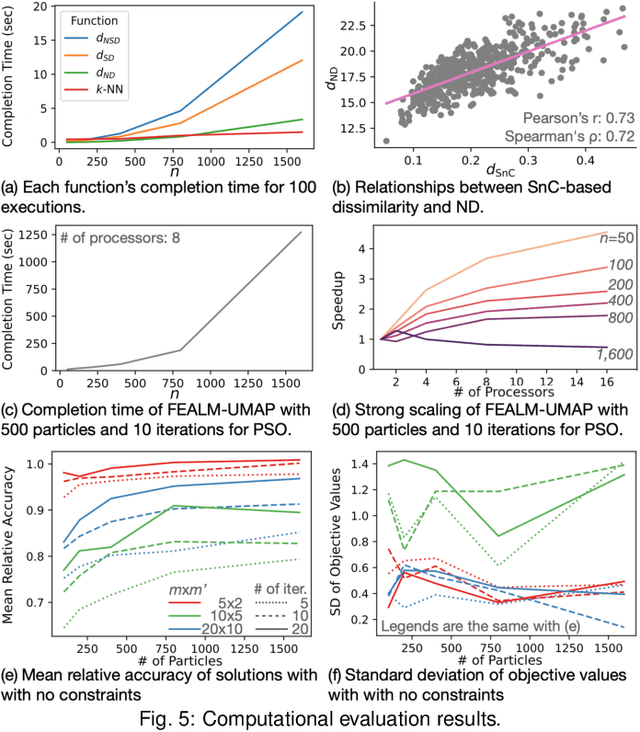
Dimensionality reduction (DR) plays a vital role in the visual analysis of high-dimensional data. One main aim of DR is to reveal hidden patterns that lie on intrinsic low-dimensional manifolds. However, DR often overlooks important patterns when the manifolds are strongly distorted or hidden by certain influential data attributes. This paper presents a feature learning framework, FEALM, designed to generate an optimized set of data projections for nonlinear DR in order to capture important patterns in the hidden manifolds. These projections produce maximally different nearest-neighbor graphs so that resultant DR outcomes are significantly different. To achieve such a capability, we design an optimization algorithm as well as introduce a new graph dissimilarity measure, called neighbor-shape dissimilarity. Additionally, we develop interactive visualizations to assist comparison of obtained DR results and interpretation of each DR result. We demonstrate FEALM's effectiveness through experiments using synthetic datasets and multiple case studies on real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge