No Free Lunch Theorem for Privacy-Preserving LLM Inference

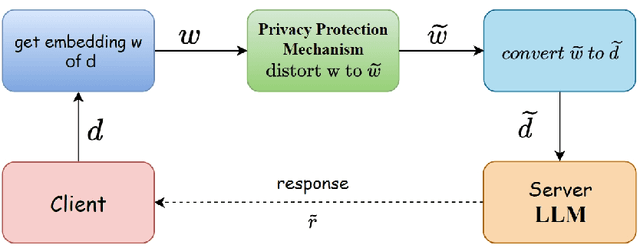
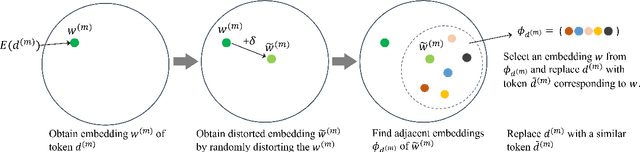
Individuals and businesses have been significantly benefited by Large Language Models (LLMs) including PaLM, Gemini and ChatGPT in various ways. For example, LLMs enhance productivity, reduce costs, and enable us to focus on more valuable tasks. Furthermore, LLMs possess the capacity to sift through extensive datasets, uncover underlying patterns, and furnish critical insights that propel the frontiers of technology and science. However, LLMs also pose privacy concerns. Users' interactions with LLMs may expose their sensitive personal or company information. A lack of robust privacy safeguards and legal frameworks could permit the unwarranted intrusion or improper handling of individual data, thereby risking infringements of privacy and the theft of personal identities. To ensure privacy, it is essential to minimize the dependency between shared prompts and private information. Various randomization approaches have been proposed to protect prompts' privacy, but they may incur utility loss compared to unprotected LLMs prompting. Therefore, it is essential to evaluate the balance between the risk of privacy leakage and loss of utility when conducting effective protection mechanisms. The current study develops a framework for inferring privacy-protected Large Language Models (LLMs) and lays down a solid theoretical basis for examining the interplay between privacy preservation and utility. The core insight is encapsulated within a theorem that is called as the NFL (abbreviation of the word No-Free-Lunch) Theorem.

Deciphering the Interplay between Local Differential Privacy, Average Bayesian Privacy, and Maximum Bayesian Privacy

The swift evolution of machine learning has led to emergence of various definitions of privacy due to the threats it poses to privacy, including the concept of local differential privacy (LDP). Although widely embraced and utilized across numerous domains, this conventional approach to measure privacy still exhibits certain limitations, spanning from failure to prevent inferential disclosure to lack of consideration for the adversary's background knowledge. In this comprehensive study, we introduce Bayesian privacy and delve into the intricate relationship between LDP and its Bayesian counterparts, unveiling novel insights into utility-privacy trade-offs. We introduce a framework that encapsulates both attack and defense strategies, highlighting their interplay and effectiveness. The relationship between LDP and Maximum Bayesian Privacy (MBP) is first revealed, demonstrating that under uniform prior distribution, a mechanism satisfying $\xi$-LDP will satisfy $\xi$-MBP and conversely $\xi$-MBP also confers 2$\xi$-LDP. Our next theoretical contribution are anchored in the rigorous definitions and relationships between Average Bayesian Privacy (ABP) and Maximum Bayesian Privacy (MBP), encapsulated by equations $\epsilon_{p,a} \leq \frac{1}{\sqrt{2}}\sqrt{(\epsilon_{p,m} + \epsilon)\cdot(e^{\epsilon_{p,m} + \epsilon} - 1)}$. These relationships fortify our understanding of the privacy guarantees provided by various mechanisms. Our work not only lays the groundwork for future empirical exploration but also promises to facilitate the design of privacy-preserving algorithms, thereby fostering the development of trustworthy machine learning solutions.