Yuanzhang Su
Multiple Partitions Aligned Clustering
Sep 13, 2019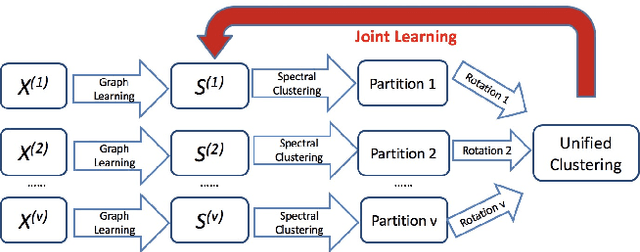


Abstract:Multi-view clustering is an important yet challenging task due to the difficulty of integrating the information from multiple representations. Most existing multi-view clustering methods explore the heterogeneous information in the space where the data points lie. Such common practice may cause significant information loss because of unavoidable noise or inconsistency among views. Since different views admit the same cluster structure, the natural space should be all partitions. Orthogonal to existing techniques, in this paper, we propose to leverage the multi-view information by fusing partitions. Specifically, we align each partition to form a consensus cluster indicator matrix through a distinct rotation matrix. Moreover, a weight is assigned for each view to account for the clustering capacity differences of views. Finally, the basic partitions, weights, and consensus clustering are jointly learned in a unified framework. We demonstrate the effectiveness of our approach on several real datasets, where significant improvement is found over other state-of-the-art multi-view clustering methods.
Latent Multi-view Semi-Supervised Classification
Sep 09, 2019
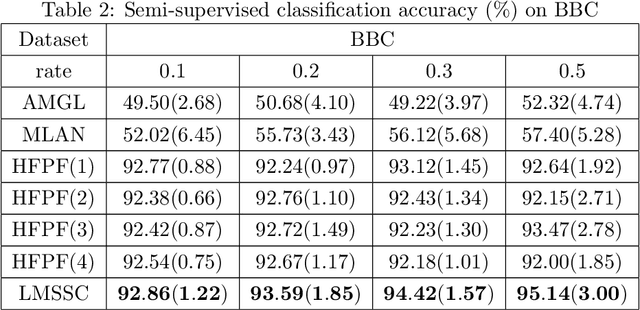
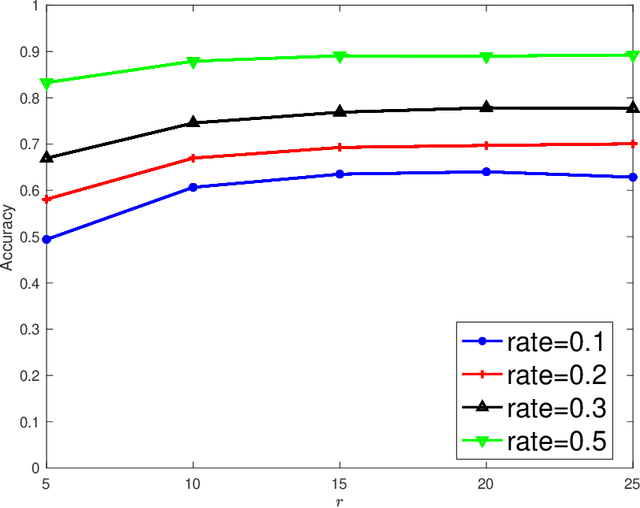
Abstract:To explore underlying complementary information from multiple views, in this paper, we propose a novel Latent Multi-view Semi-Supervised Classification (LMSSC) method. Unlike most existing multi-view semi-supervised classification methods that learn the graph using original features, our method seeks an underlying latent representation and performs graph learning and label propagation based on the learned latent representation. With the complementarity of multiple views, the latent representation could depict the data more comprehensively than every single view individually, accordingly making the graph more accurate and robust as well. Finally, LMSSC integrates latent representation learning, graph construction, and label propagation into a unified framework, which makes each subtask optimized. Experimental results on real-world benchmark datasets validate the effectiveness of our proposed method.
Similarity Learning via Kernel Preserving Embedding
Mar 11, 2019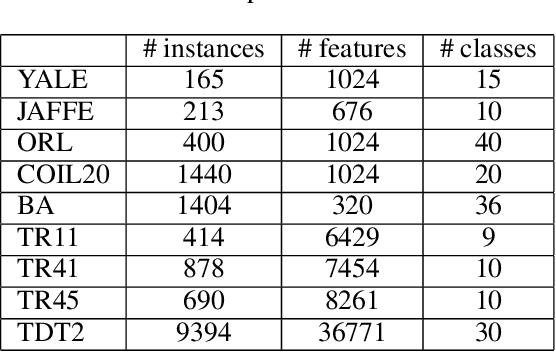

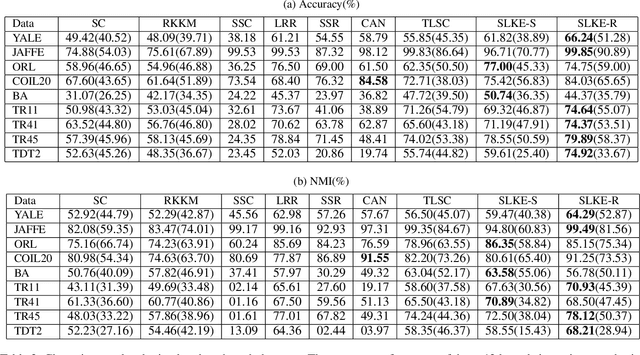

Abstract:Data similarity is a key concept in many data-driven applications. Many algorithms are sensitive to similarity measures. To tackle this fundamental problem, automatically learning of similarity information from data via self-expression has been developed and successfully applied in various models, such as low-rank representation, sparse subspace learning, semi-supervised learning. However, it just tries to reconstruct the original data and some valuable information, e.g., the manifold structure, is largely ignored. In this paper, we argue that it is beneficial to preserve the overall relations when we extract similarity information. Specifically, we propose a novel similarity learning framework by minimizing the reconstruction error of kernel matrices, rather than the reconstruction error of original data adopted by existing work. Taking the clustering task as an example to evaluate our method, we observe considerable improvements compared to other state-of-the-art methods. More importantly, our proposed framework is very general and provides a novel and fundamental building block for many other similarity-based tasks. Besides, our proposed kernel preserving opens up a large number of possibilities to embed high-dimensional data into low-dimensional space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge