Cyclic and Randomized Stepsizes Invoke Heavier Tails in SGD

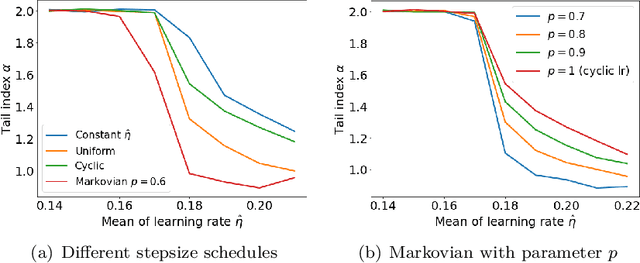
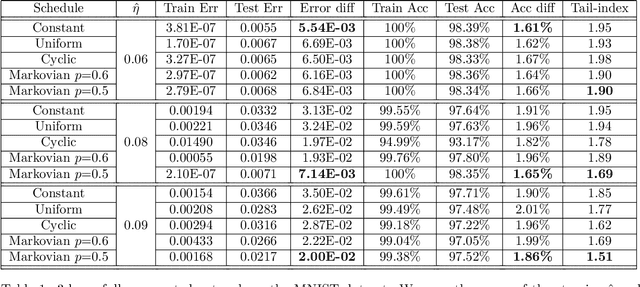
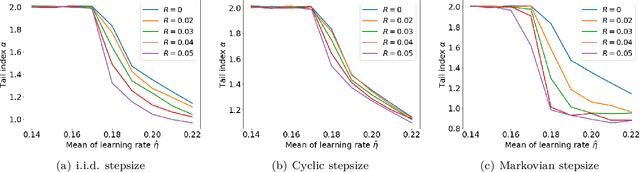
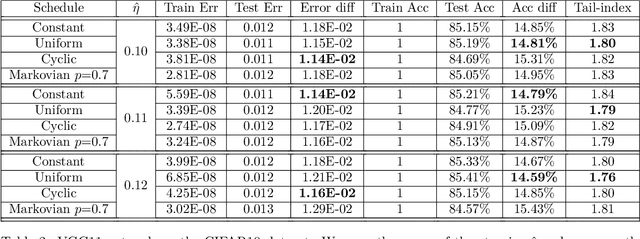
Cyclic and randomized stepsizes are widely used in the deep learning practice and can often outperform standard stepsize choices such as constant stepsize in SGD. Despite their empirical success, not much is currently known about when and why they can theoretically improve the generalization performance. We consider a general class of Markovian stepsizes for learning, which contain i.i.d. random stepsize, cyclic stepsize as well as the constant stepsize as special cases, and motivated by the literature which shows that heaviness of the tails (measured by the so-called "tail-index") in the SGD iterates is correlated with generalization, we study tail-index and provide a number of theoretical results that demonstrate how the tail-index varies on the stepsize scheduling. Our results bring a new understanding of the benefits of cyclic and randomized stepsizes compared to constant stepsize in terms of the tail behavior. We illustrate our theory on linear regression experiments and show through deep learning experiments that Markovian stepsizes can achieve even a heavier tail and be a viable alternative to cyclic and i.i.d. randomized stepsize rules.

Penalized Langevin and Hamiltonian Monte Carlo Algorithms for Constrained Sampling

We consider the constrained sampling problem where the goal is to sample from a distribution $\pi(x)\propto e^{-f(x)}$ and $x$ is constrained on a convex body $\mathcal{C}\subset \mathbb{R}^d$. Motivated by penalty methods from optimization, we propose penalized Langevin Dynamics (PLD) and penalized Hamiltonian Monte Carlo (PHMC) that convert the constrained sampling problem into an unconstrained one by introducing a penalty function for constraint violations. When $f$ is smooth and the gradient is available, we show $\tilde{\mathcal{O}}(d/\varepsilon^{10})$ iteration complexity for PLD to sample the target up to an $\varepsilon$-error where the error is measured in terms of the total variation distance and $\tilde{\mathcal{O}}(\cdot)$ hides some logarithmic factors. For PHMC, we improve this result to $\tilde{\mathcal{O}}(\sqrt{d}/\varepsilon^{7})$ when the Hessian of $f$ is Lipschitz and the boundary of $\mathcal{C}$ is sufficiently smooth. To our knowledge, these are the first convergence rate results for Hamiltonian Monte Carlo methods in the constrained sampling setting that can handle non-convex $f$ and can provide guarantees with the best dimension dependency among existing methods with deterministic gradients. We then consider the setting where unbiased stochastic gradients are available. We propose PSGLD and PSGHMC that can handle stochastic gradients without Metropolis-Hasting correction steps. When $f$ is strongly convex and smooth, we obtain an iteration complexity of $\tilde{\mathcal{O}}(d/\varepsilon^{18})$ and $\tilde{\mathcal{O}}(d\sqrt{d}/\varepsilon^{39})$ respectively in the 2-Wasserstein distance. For the more general case, when $f$ is smooth and non-convex, we also provide finite-time performance bounds and iteration complexity results. Finally, we test our algorithms on Bayesian LASSO regression and Bayesian constrained deep learning problems.

Heavy-Tail Phenomenon in Decentralized SGD

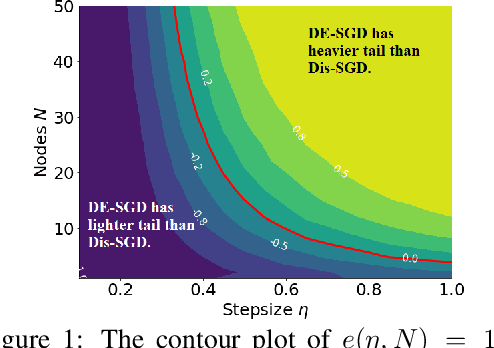
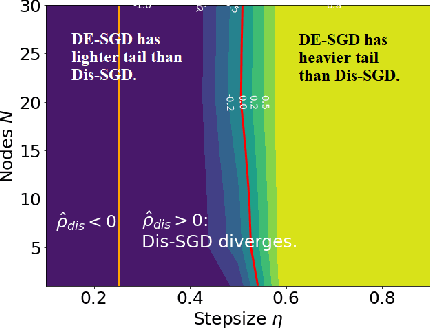
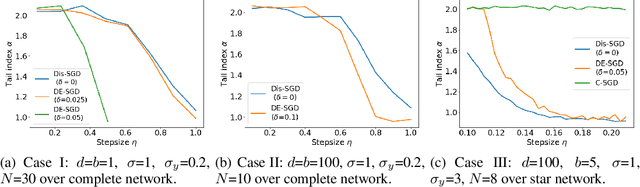
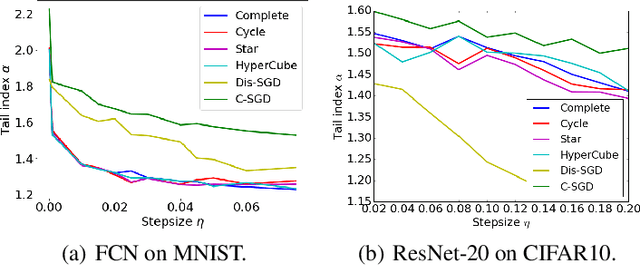
Recent theoretical studies have shown that heavy-tails can emerge in stochastic optimization due to `multiplicative noise', even under surprisingly simple settings, such as linear regression with Gaussian data. While these studies have uncovered several interesting phenomena, they consider conventional stochastic optimization problems, which exclude decentralized settings that naturally arise in modern machine learning applications. In this paper, we study the emergence of heavy-tails in decentralized stochastic gradient descent (DE-SGD), and investigate the effect of decentralization on the tail behavior. We first show that, when the loss function at each computational node is twice continuously differentiable and strongly convex outside a compact region, the law of the DE-SGD iterates converges to a distribution with polynomially decaying (heavy) tails. To have a more explicit control on the tail exponent, we then consider the case where the loss at each node is a quadratic, and show that the tail-index can be estimated as a function of the step-size, batch-size, and the topological properties of the network of the computational nodes. Then, we provide theoretical and empirical results showing that DE-SGD has heavier tails than centralized SGD. We also compare DE-SGD to disconnected SGD where nodes distribute the data but do not communicate. Our theory uncovers an interesting interplay between the tails and the network structure: we identify two regimes of parameters (stepsize and network size), where DE-SGD can have lighter or heavier tails than disconnected SGD depending on the regime. Finally, to support our theoretical results, we provide numerical experiments conducted on both synthetic data and neural networks.

Decentralized Stochastic Gradient Langevin Dynamics and Hamiltonian Monte Carlo

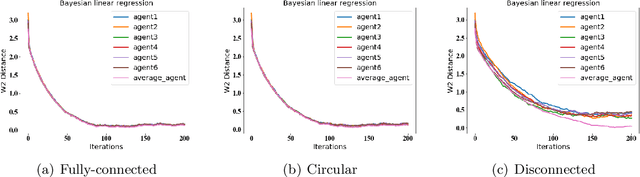
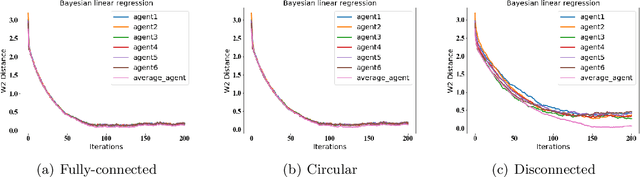
Stochastic gradient Langevin dynamics (SGLD) and stochastic gradient Hamiltonian Monte Carlo (SGHMC) are two popular Markov Chain Monte Carlo (MCMC) algorithms for Bayesian inference that can scale to large datasets, allowing to sample from the posterior distribution of a machine learning (ML) model based on the input data and the prior distribution over the model parameters. However, these algorithms do not apply to the decentralized learning setting, when a network of agents are working collaboratively to learn the parameters of an ML model without sharing their individual data due to privacy reasons or communication constraints. We study two algorithms: Decentralized SGLD (DE-SGLD) and Decentralized SGHMC (DE-SGHMC) which are adaptations of SGLD and SGHMC methods that allow scaleable Bayesian inference in the decentralized setting. We show that when the posterior distribution is strongly log-concave, the iterates of these algorithms converge linearly to a neighborhood of the target distribution in the 2-Wasserstein metric. We illustrate the results for decentralized Bayesian linear regression and Bayesian logistic regression problems.

Fractional moment-preserving initialization schemes for training fully-connected neural networks

A traditional approach to initialization in deep neural networks (DNNs) is to sample the network weights randomly for preserving the variance of pre-activations. On the other hand, several studies show that during the training process, the distribution of stochastic gradients can be heavy-tailed especially for small batch sizes. In this case, weights and therefore pre-activations can be modeled with a heavy-tailed distribution that has an infinite variance but has a finite (non-integer) fractional moment of order $s$ with $s<2$. Motivated by this fact, we develop initialization schemes for fully connected feed-forward networks that can provably preserve any given moment of order $s \in (0, 2]$ over the layers for a class of activations including ReLU, Leaky ReLU, Randomized Leaky ReLU, and linear activations. These generalized schemes recover traditional initialization schemes in the limit $s \to 2$ and serve as part of a principled theory for initialization. For all these schemes, we show that the network output admits a finite almost sure limit as the number of layers grows, and the limit is heavy-tailed in some settings. This sheds further light into the origins of heavy tail during signal propagation in DNNs. We prove that the logarithm of the norm of the network outputs, if properly scaled, will converge to a Gaussian distribution with an explicit mean and variance we can compute depending on the activation used, the value of s chosen and the network width. We also prove that our initialization scheme avoids small network output values more frequently compared to traditional approaches. Furthermore, the proposed initialization strategy does not have an extra cost during the training procedure. We show through numerical experiments that our initialization can improve the training and test performance.

Non-Convex Stochastic Optimization via Non-Reversible Stochastic Gradient Langevin Dynamics

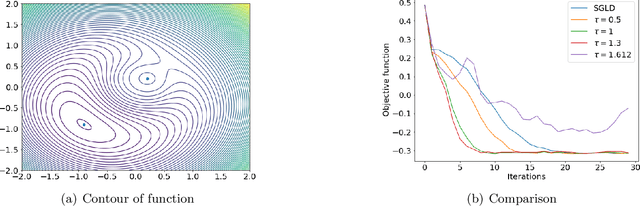
Stochastic gradient Langevin dynamics (SGLD) is a poweful algorithm for optimizing a non-convex objective, where a controlled and properly scaled Gaussian noise is added to the stochastic gradients to steer the iterates towards a global minimum. SGLD is based on the overdamped Langevin diffusion which is reversible in time. By adding an anti-symmetric matrix to the drift term of the overdamped Langevin diffusion, one gets a non-reversible diffusion that converges to the same stationary distribution with a faster convergence rate. In this paper, we study the non-reversible stochastic gradient Langevin dynamics (NSGLD) which is based on discretization of the non-reversible Langevin diffusion. We provide finite time performance bounds for the global convergence of NSGLD for solving stochastic non-convex optimization problems. Our results lead to non-asymptotic guarantees for both population and empirical risk minimization problems. Numerical experiments for a simple polynomial function optimization, Bayesian independent component analysis and neural network models show that NSGLD can outperform SGLD with proper choices of the anti-symmetric matrix.