Experimental robustness benchmark of quantum neural network on a superconducting quantum processor

Quantum machine learning (QML) models, like their classical counterparts, are vulnerable to adversarial attacks, hindering their secure deployment. Here, we report the first systematic experimental robustness benchmark for 20-qubit quantum neural network (QNN) classifiers executed on a superconducting processor. Our benchmarking framework features an efficient adversarial attack algorithm designed for QNNs, enabling quantitative characterization of adversarial robustness and robustness bounds. From our analysis, we verify that adversarial training reduces sensitivity to targeted perturbations by regularizing input gradients, significantly enhancing QNN's robustness. Additionally, our analysis reveals that QNNs exhibit superior adversarial robustness compared to classical neural networks, an advantage attributed to inherent quantum noise. Furthermore, the empirical upper bound extracted from our attack experiments shows a minimal deviation ($3 \times 10^{-3}$) from the theoretical lower bound, providing strong experimental confirmation of the attack's effectiveness and the tightness of fidelity-based robustness bounds. This work establishes a critical experimental framework for assessing and improving quantum adversarial robustness, paving the way for secure and reliable QML applications.

Statistics-Informed Parameterized Quantum Circuit via Maximum Entropy Principle for Data Science and Finance

Quantum machine learning has demonstrated significant potential in solving practical problems, particularly in statistics-focused areas such as data science and finance. However, challenges remain in preparing and learning statistical models on a quantum processor due to issues with trainability and interpretability. In this letter, we utilize the maximum entropy principle to design a statistics-informed parameterized quantum circuit (SI-PQC) that efficiently prepares and trains quantum computational statistical models, including arbitrary distributions and their weighted mixtures. The SI-PQC features a static structure with trainable parameters, enabling in-depth optimized circuit compilation, exponential reductions in resource and time consumption, and improved trainability and interpretability for learning quantum states and classical model parameters simultaneously. As an efficient subroutine for preparing and learning in various quantum algorithms, the SI-PQC addresses the input bottleneck and facilitates the injection of prior knowledge.

Experimentally detecting a quantum change point via Bayesian inference

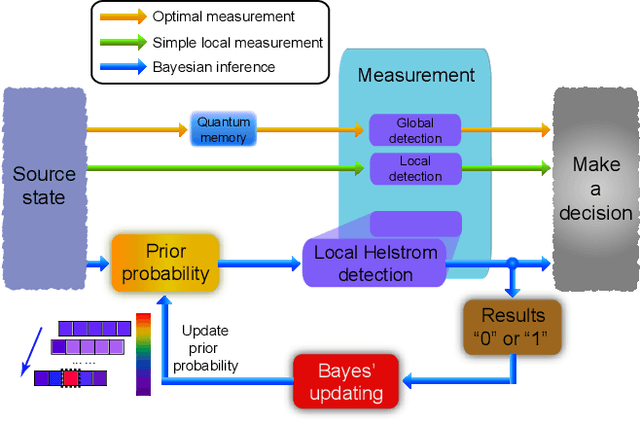
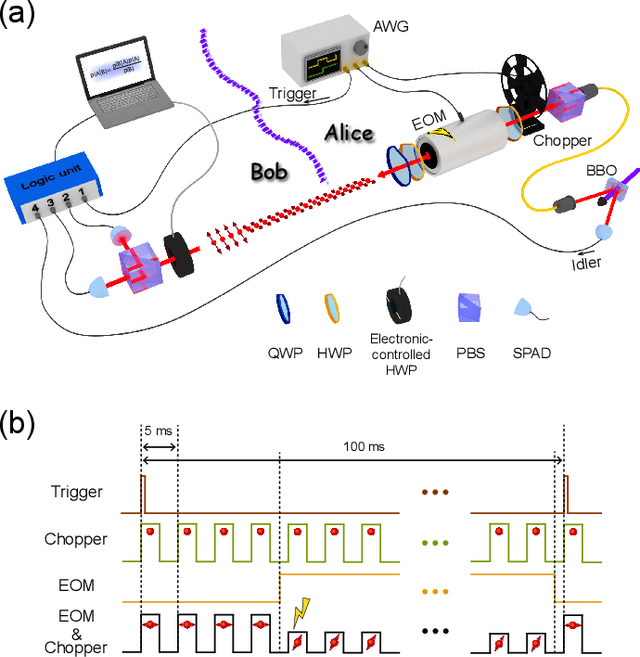
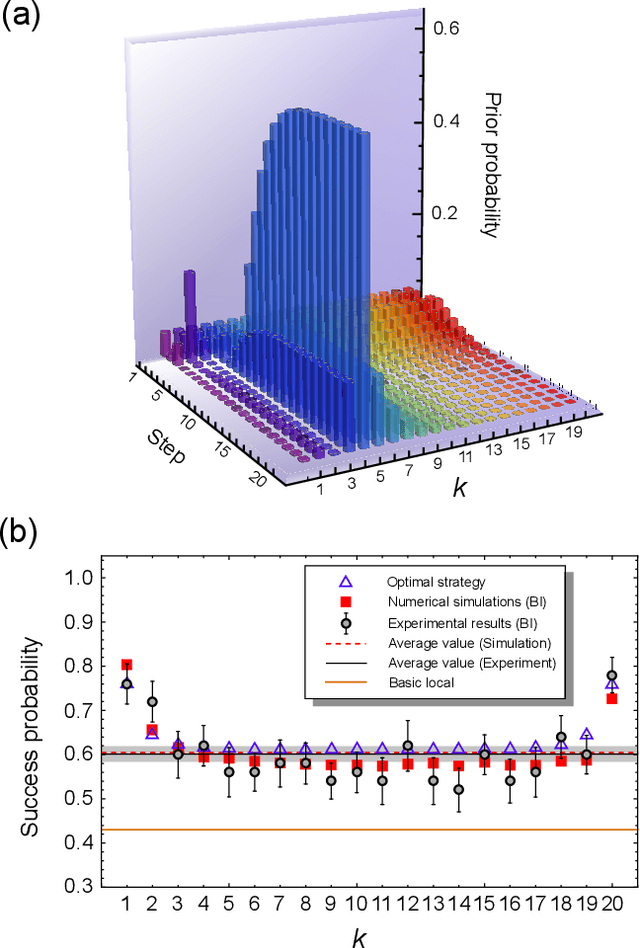
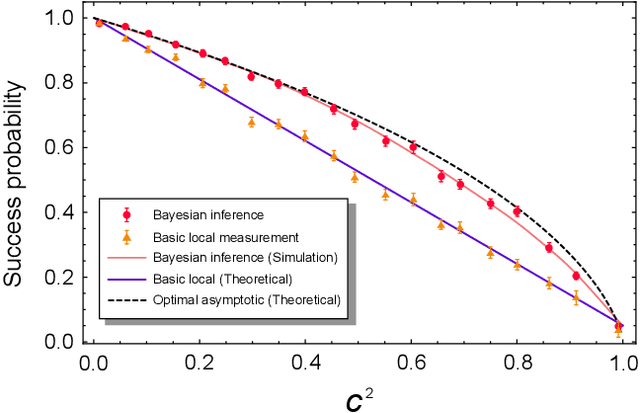
Detecting a change point is a crucial task in statistics that has been recently extended to the quantum realm. A source state generator that emits a series of single photons in a default state suffers an alteration at some point and starts to emit photons in a mutated state. The problem consists in identifying the point where the change took place. In this work, we consider a learning agent that applies Bayesian inference on experimental data to solve this problem. This learning machine adjusts the measurement over each photon according to the past experimental results finds the change position in an online fashion. Our results show that the local-detection success probability can be largely improved by using such a machine learning technique. This protocol provides a tool for improvement in many applications where a sequence of identical quantum states is required.