Learning Adaptive and View-Invariant Vision Transformer with Multi-Teacher Knowledge Distillation for Real-Time UAV Tracking

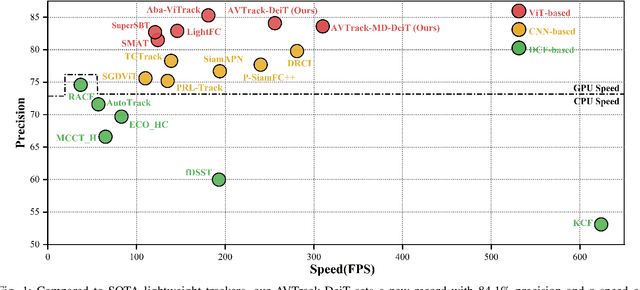
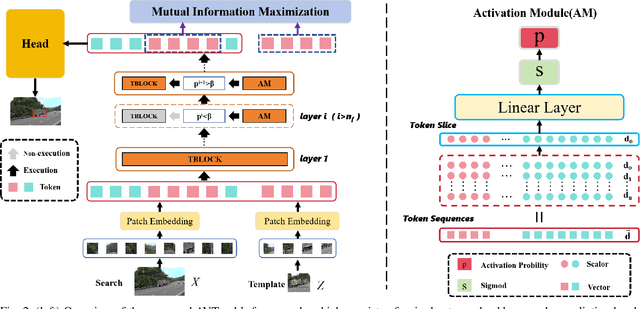
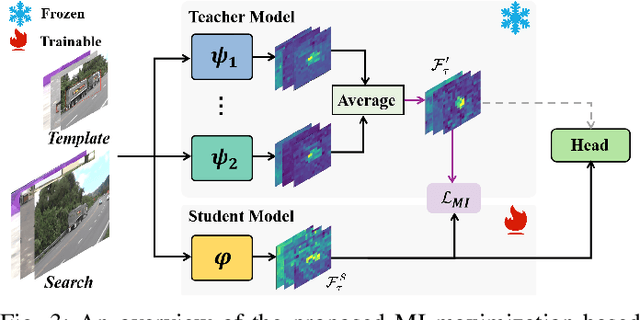
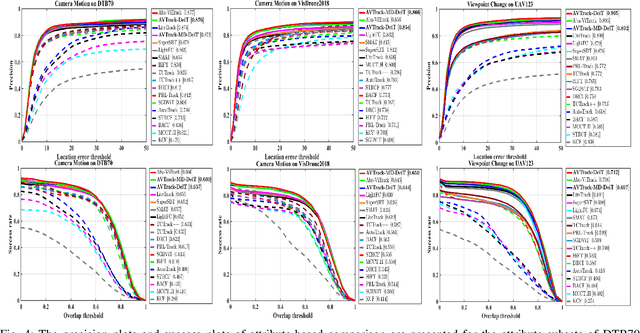
Visual tracking has made significant strides due to the adoption of transformer-based models. Most state-of-the-art trackers struggle to meet real-time processing demands on mobile platforms with constrained computing resources, particularly for real-time unmanned aerial vehicle (UAV) tracking. To achieve a better balance between performance and efficiency, we introduce AVTrack, an adaptive computation framework designed to selectively activate transformer blocks for real-time UAV tracking. The proposed Activation Module (AM) dynamically optimizes the ViT architecture by selectively engaging relevant components, thereby enhancing inference efficiency without significant compromise to tracking performance. Furthermore, to tackle the challenges posed by extreme changes in viewing angles often encountered in UAV tracking, the proposed method enhances ViTs' effectiveness by learning view-invariant representations through mutual information (MI) maximization. Two effective design principles are proposed in the AVTrack. Building on it, we propose an improved tracker, dubbed AVTrack-MD, which introduces the novel MI maximization-based multi-teacher knowledge distillation (MD) framework. It harnesses the benefits of multiple teachers, specifically the off-the-shelf tracking models from the AVTrack, by integrating and refining their outputs, thereby guiding the learning process of the compact student network. Specifically, we maximize the MI between the softened feature representations from the multi-teacher models and the student model, leading to improved generalization and performance of the student model, particularly in noisy conditions. Extensive experiments on multiple UAV tracking benchmarks demonstrate that AVTrack-MD not only achieves performance comparable to the AVTrack baseline but also reduces model complexity, resulting in a significant 17\% increase in average tracking speed.

An Efficient Approach to Regression Problems with Tensor Neural Networks

This paper introduces a tensor neural network (TNN) to address nonparametric regression problems. Characterized by its distinct sub-network structure, the TNN effectively facilitates variable separation, thereby enhancing the approximation of complex, unknown functions. Our comparative analysis reveals that the TNN outperforms conventional Feed-Forward Networks (FFN) and Radial Basis Function Networks (RBN) in terms of both approximation accuracy and generalization potential, despite a similar scale of parameters. A key innovation of our approach is the integration of statistical regression and numerical integration within the TNN framework. This integration allows for the efficient computation of high-dimensional integrals associated with the regression function. The implications of this advancement extend to a broader range of applications, particularly in scenarios demanding precise high-dimensional data analysis and prediction.

The Infinity of Randomness

This work starts from definition of randomness, the results of algorithmic randomness are analyzed from the perspective of application. Then, the source and nature of randomness is explored, and the relationship between infinity and randomness is found. The properties of randomness are summarized from the perspective of interaction between systems, that is, the set composed of sequences generated by randomness has the property of asymptotic completeness. Finally, the importance of randomness in AI research is emphasized.