IQNAS: Interpretable Integer Quadratic Programming Neural Architecture Search

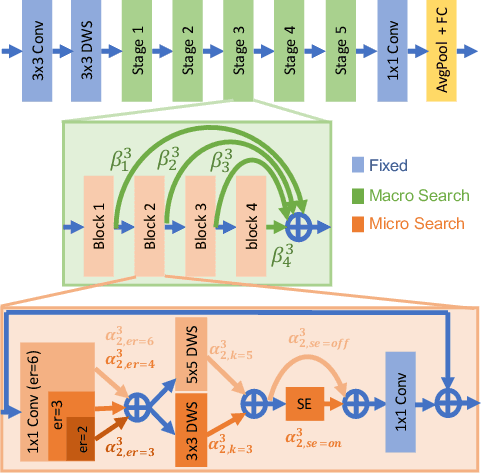
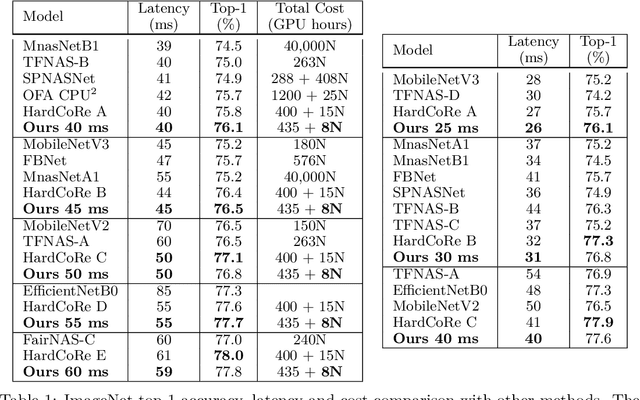
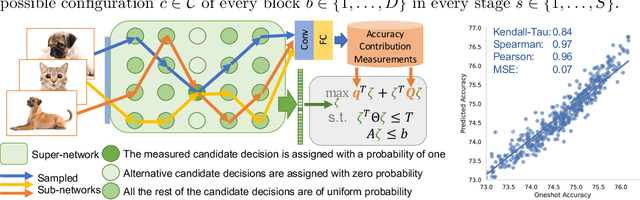
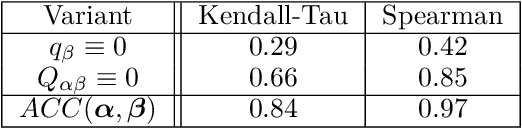
Realistic use of neural networks often requires adhering to multiple constraints on latency, energy and memory among others. A popular approach to find fitting networks is through constrained Neural Architecture Search (NAS). However, previous methods use complicated predictors for the accuracy of the network. Those predictors are hard to interpret and sensitive to many hyperparameters to be tuned, hence, the resulting accuracy of the generated models is often harmed. In this work we resolve this by introducing Interpretable Integer Quadratic programming Neural Architecture Search (IQNAS), that is based on an accurate and simple quadratic formulation of both the accuracy predictor and the expected resource requirement, together with a scalable search method with theoretical guarantees. The simplicity of our proposed predictor together with the intuitive way it is constructed bring interpretability through many insights about the contribution of different design choices. For example, we find that in the examined search space, adding depth and width is more effective at deeper stages of the network and at the beginning of each resolution stage. Our experiments show that IQNAS generates comparable to or better architectures than other state-of-the-art NAS methods within a reduced search cost for each additional generated network, while strictly satisfying the resource constraints.

HardCoRe-NAS: Hard Constrained diffeRentiable Neural Architecture Search

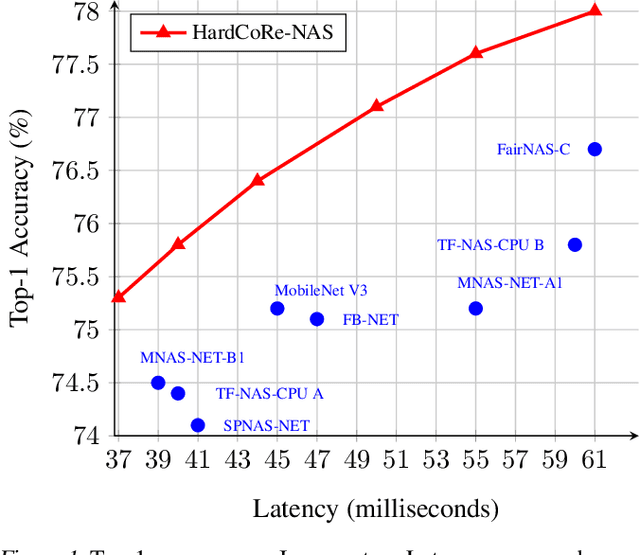
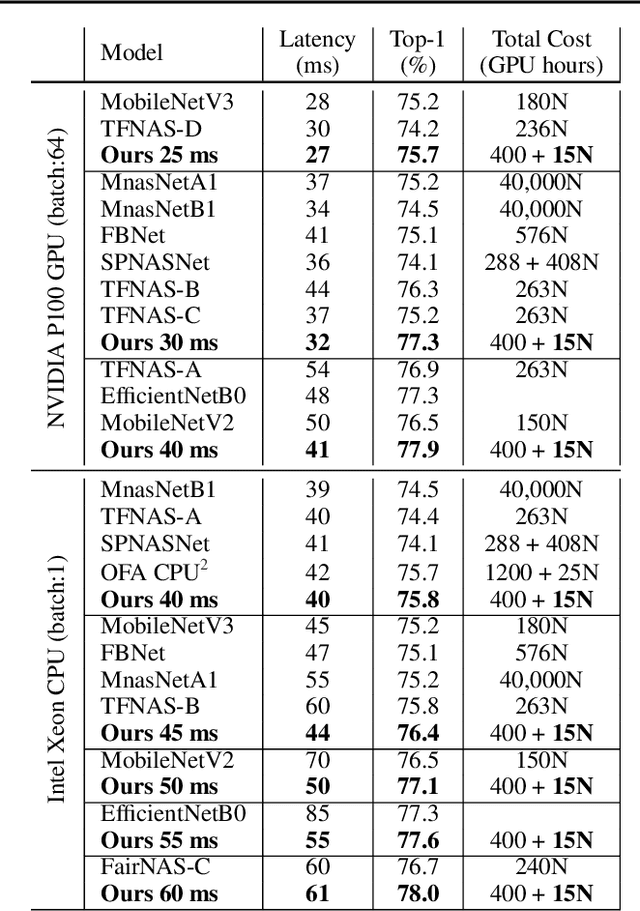
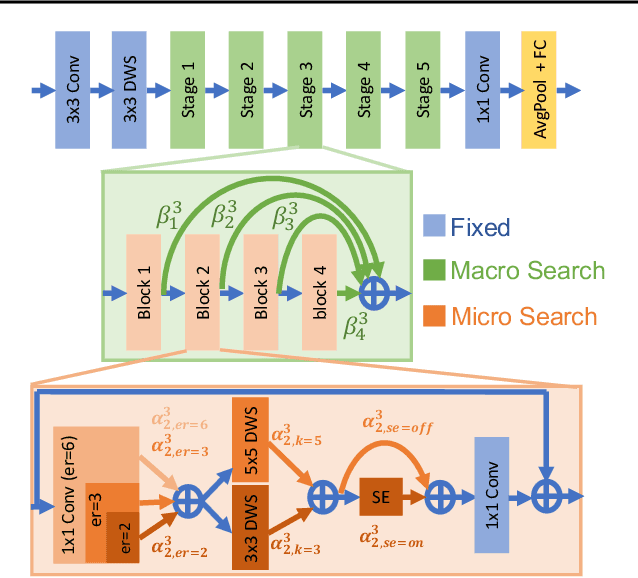
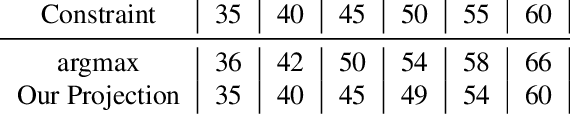
Realistic use of neural networks often requires adhering to multiple constraints on latency, energy and memory among others. A popular approach to find fitting networks is through constrained Neural Architecture Search (NAS), however, previous methods enforce the constraint only softly. Therefore, the resulting networks do not exactly adhere to the resource constraint and their accuracy is harmed. In this work we resolve this by introducing Hard Constrained diffeRentiable NAS (HardCoRe-NAS), that is based on an accurate formulation of the expected resource requirement and a scalable search method that satisfies the hard constraint throughout the search. Our experiments show that HardCoRe-NAS generates state-of-the-art architectures, surpassing other NAS methods, while strictly satisfying the hard resource constraints without any tuning required.

A Convergence Theory Towards Practical Over-parameterized Deep Neural Networks

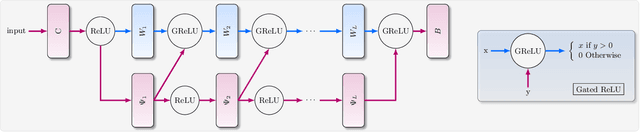
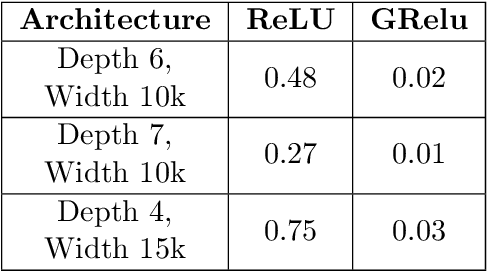
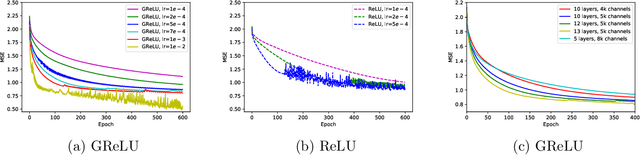
Deep neural networks' remarkable ability to correctly fit training data when optimized by gradient-based algorithms is yet to be fully understood. Recent theoretical results explain the convergence for ReLU networks that are wider than those used in practice by orders of magnitude. In this work, we take a step towards closing the gap between theory and practice by significantly improving the known theoretical bounds on both the network width and the convergence time. We show that convergence to a global minimum is guaranteed for networks with widths quadratic in the sample size and linear in their depth at a time logarithmic in both. Our analysis and convergence bounds are derived via the construction of a surrogate network with fixed activation patterns that can be transformed at any time to an equivalent ReLU network of a reasonable size. This construction can be viewed as a novel technique to accelerate training, while its tight finite-width equivalence to Neural Tangent Kernel (NTK) suggests it can be utilized to study generalization as well.

Knapsack Pruning with Inner Distillation

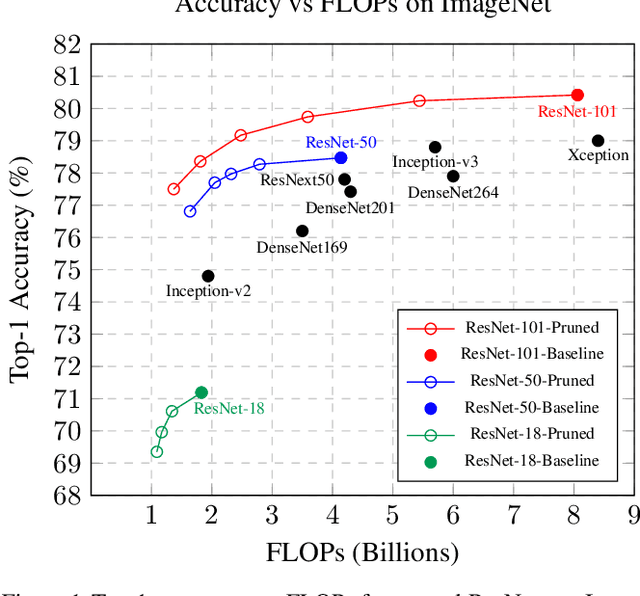
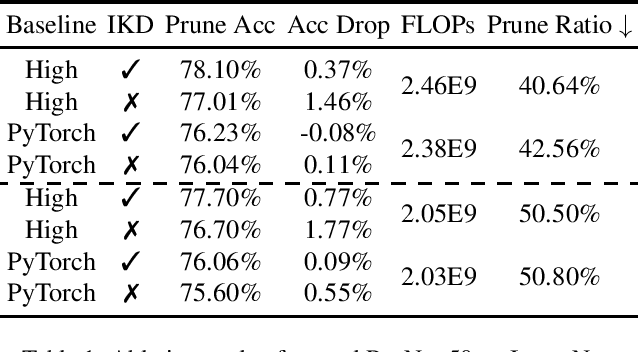
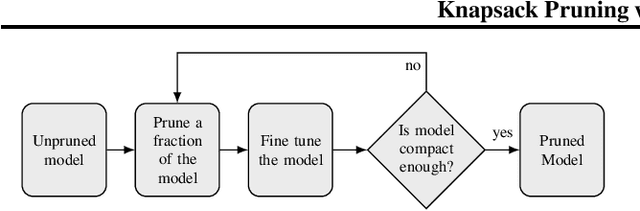
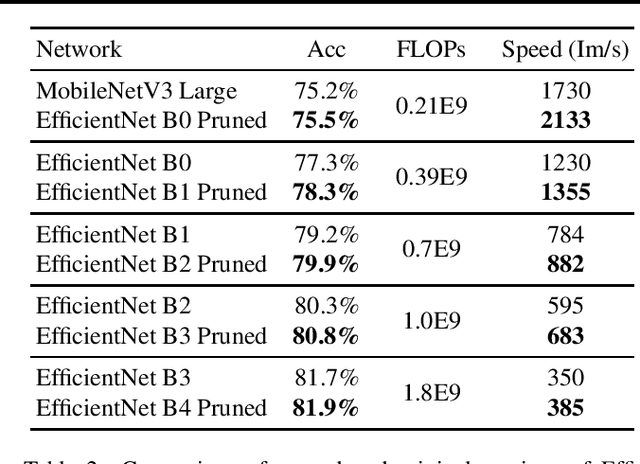
Neural network pruning reduces the computational cost of an over-parameterized network to improve its efficiency. Popular methods vary from $\ell_1$-norm sparsification to Neural Architecture Search (NAS). In this work, we propose a novel pruning method that optimizes the final accuracy of the pruned network and distills knowledge from the over-parameterized parent network's inner layers. To enable this approach, we formulate the network pruning as a Knapsack Problem which optimizes the trade-off between the importance of neurons and their associated computational cost. Then we prune the network channels while maintaining the high-level structure of the network. The pruned network is fine-tuned under the supervision of the parent network using its inner network knowledge, a technique we refer to as the Inner Knowledge Distillation. Our method leads to state-of-the-art pruning results on ImageNet, CIFAR-10 and CIFAR-100 using ResNet backbones. To prune complex network structures such as convolutions with skip-links and depth-wise convolutions, we propose a block grouping approach to cope with these structures. Through this we produce compact architectures with the same FLOPs as EfficientNet-B0 and MobileNetV3 but with higher accuracy, by $1\%$ and $0.3\%$ respectively on ImageNet, and faster runtime on GPU.

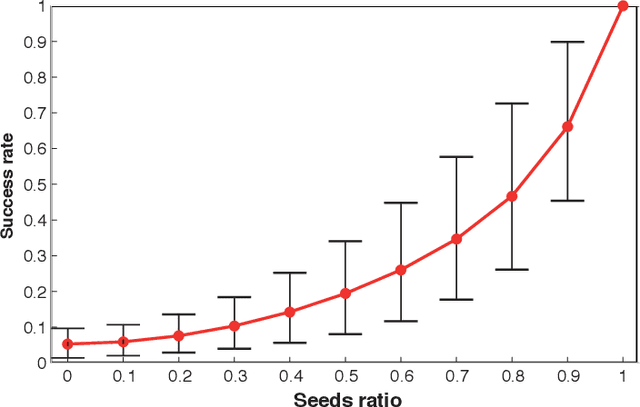
Graph matching: relax or not?

We consider the problem of exact and inexact matching of weighted undirected graphs, in which a bijective correspondence is sought to minimize a quadratic weight disagreement. This computationally challenging problem is often relaxed as a convex quadratic program, in which the space of permutations is replaced by the space of doubly-stochastic matrices. However, the applicability of such a relaxation is poorly understood. We define a broad class of friendly graphs characterized by an easily verifiable spectral property. We prove that for friendly graphs, the convex relaxation is guaranteed to find the exact isomorphism or certify its inexistence. This result is further extended to approximately isomorphic graphs, for which we develop an explicit bound on the amount of weight disagreement under which the relaxation is guaranteed to find the globally optimal approximate isomorphism. We also show that in many cases, the graph matching problem can be further harmlessly relaxed to a convex quadratic program with only n separable linear equality constraints, which is substantially more efficient than the standard relaxation involving 2n equality and n^2 inequality constraints. Finally, we show that our results are still valid for unfriendly graphs if additional information in the form of seeds or attributes is allowed, with the latter satisfying an easy to verify spectral characteristic.

On the optimality of shape and data representation in the spectral domain

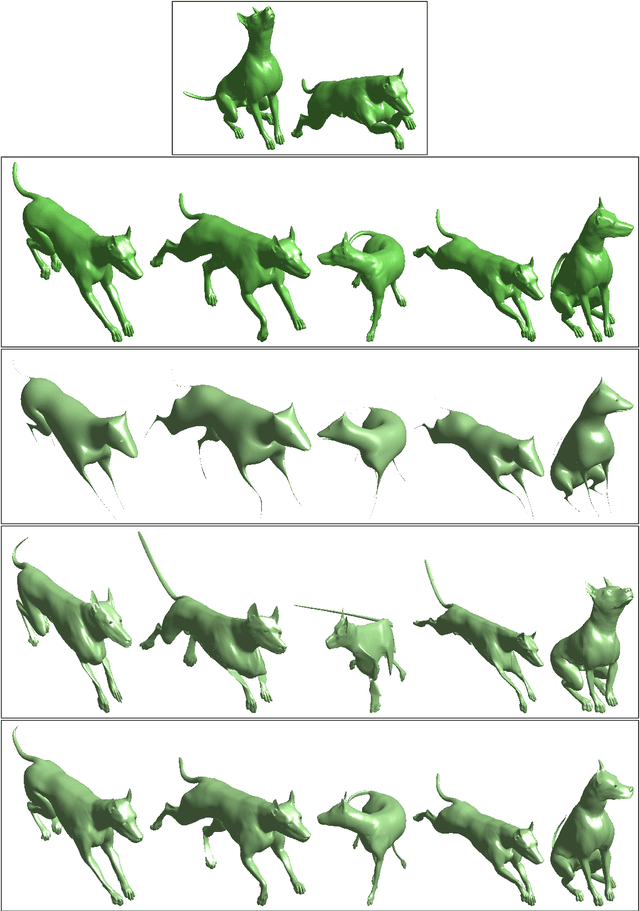
A proof of the optimality of the eigenfunctions of the Laplace-Beltrami operator (LBO) in representing smooth functions on surfaces is provided and adapted to the field of applied shape and data analysis. It is based on the Courant-Fischer min-max principle adapted to our case. % The theorem we present supports the new trend in geometry processing of treating geometric structures by using their projection onto the leading eigenfunctions of the decomposition of the LBO. Utilisation of this result can be used for constructing numerically efficient algorithms to process shapes in their spectrum. We review a couple of applications as possible practical usage cases of the proposed optimality criteria. % We refer to a scale invariant metric, which is also invariant to bending of the manifold. This novel pseudo-metric allows constructing an LBO by which a scale invariant eigenspace on the surface is defined. We demonstrate the efficiency of an intermediate metric, defined as an interpolation between the scale invariant and the regular one, in representing geometric structures while capturing both coarse and fine details. Next, we review a numerical acceleration technique for classical scaling, a member of a family of flattening methods known as multidimensional scaling (MDS). There, the optimality is exploited to efficiently approximate all geodesic distances between pairs of points on a given surface, and thereby match and compare between almost isometric surfaces. Finally, we revisit the classical principal component analysis (PCA) definition by coupling its variational form with a Dirichlet energy on the data manifold. By pairing the PCA with the LBO we can handle cases that go beyond the scope defined by the observation set that is handled by regular PCA.