A Convergence Theory Towards Practical Over-parameterized Deep Neural Networks
Paper and Code
Feb 08, 2021
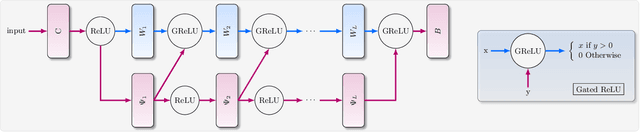
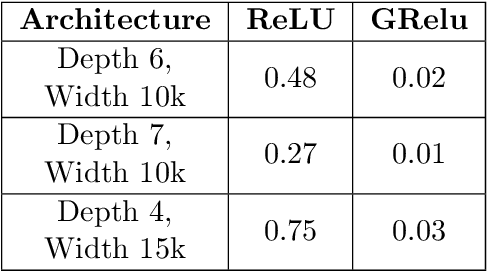
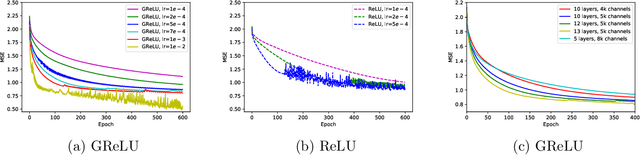
Deep neural networks' remarkable ability to correctly fit training data when optimized by gradient-based algorithms is yet to be fully understood. Recent theoretical results explain the convergence for ReLU networks that are wider than those used in practice by orders of magnitude. In this work, we take a step towards closing the gap between theory and practice by significantly improving the known theoretical bounds on both the network width and the convergence time. We show that convergence to a global minimum is guaranteed for networks with widths quadratic in the sample size and linear in their depth at a time logarithmic in both. Our analysis and convergence bounds are derived via the construction of a surrogate network with fixed activation patterns that can be transformed at any time to an equivalent ReLU network of a reasonable size. This construction can be viewed as a novel technique to accelerate training, while its tight finite-width equivalence to Neural Tangent Kernel (NTK) suggests it can be utilized to study generalization as well.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge