Yiting Yang
Efficient Adaptation of Pre-trained Vision Transformer via Householder Transformation
Oct 30, 2024
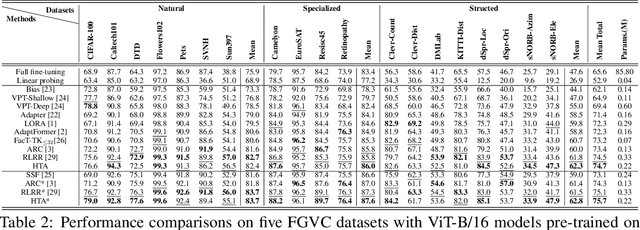

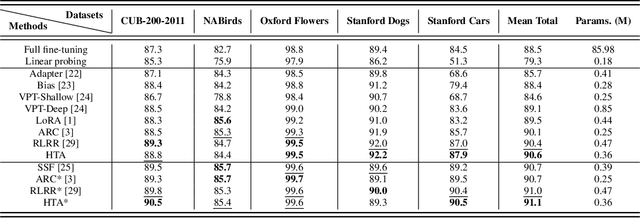
Abstract:A common strategy for Parameter-Efficient Fine-Tuning (PEFT) of pre-trained Vision Transformers (ViTs) involves adapting the model to downstream tasks by learning a low-rank adaptation matrix. This matrix is decomposed into a product of down-projection and up-projection matrices, with the bottleneck dimensionality being crucial for reducing the number of learnable parameters, as exemplified by prevalent methods like LoRA and Adapter. However, these low-rank strategies typically employ a fixed bottleneck dimensionality, which limits their flexibility in handling layer-wise variations. To address this limitation, we propose a novel PEFT approach inspired by Singular Value Decomposition (SVD) for representing the adaptation matrix. SVD decomposes a matrix into the product of a left unitary matrix, a diagonal matrix of scaling values, and a right unitary matrix. We utilize Householder transformations to construct orthogonal matrices that efficiently mimic the unitary matrices, requiring only a vector. The diagonal values are learned in a layer-wise manner, allowing them to flexibly capture the unique properties of each layer. This approach enables the generation of adaptation matrices with varying ranks across different layers, providing greater flexibility in adapting pre-trained models. Experiments on standard downstream vision tasks demonstrate that our method achieves promising fine-tuning performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge