Taming Equilibrium Bias in Risk-Sensitive Multi-Agent Reinforcement Learning

We study risk-sensitive multi-agent reinforcement learning under general-sum Markov games, where agents optimize the entropic risk measure of rewards with possibly diverse risk preferences. We show that using the regret naively adapted from existing literature as a performance metric could induce policies with equilibrium bias that favor the most risk-sensitive agents and overlook the other agents. To address such deficiency of the naive regret, we propose a novel notion of regret, which we call risk-balanced regret, and show through a lower bound that it overcomes the issue of equilibrium bias. Furthermore, we develop a self-play algorithm for learning Nash, correlated, and coarse correlated equilibria in risk-sensitive Markov games. We prove that the proposed algorithm attains near-optimal regret guarantees with respect to the risk-balanced regret.

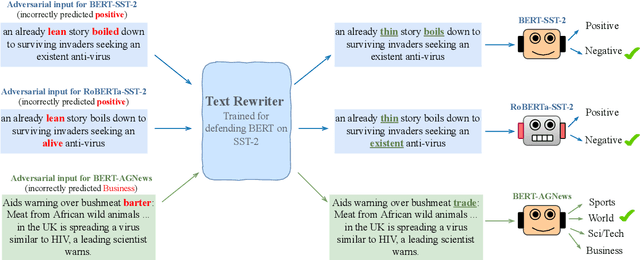
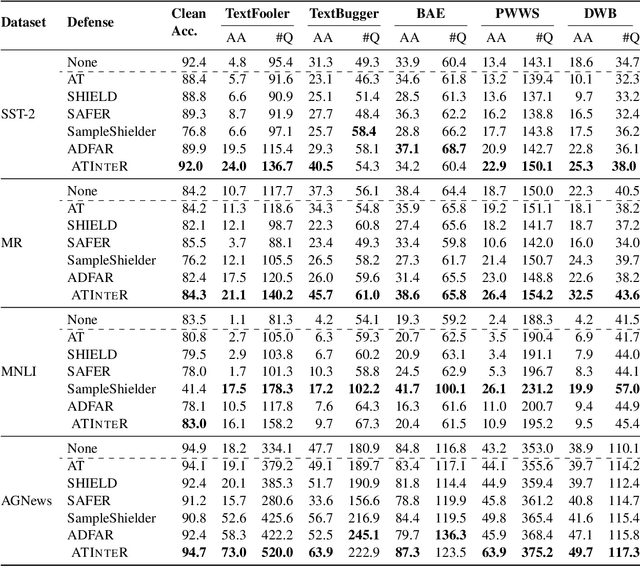
Don't Retrain, Just Rewrite: Countering Adversarial Perturbations by Rewriting Text

Can language models transform inputs to protect text classifiers against adversarial attacks? In this work, we present ATINTER, a model that intercepts and learns to rewrite adversarial inputs to make them non-adversarial for a downstream text classifier. Our experiments on four datasets and five attack mechanisms reveal that ATINTER is effective at providing better adversarial robustness than existing defense approaches, without compromising task accuracy. For example, on sentiment classification using the SST-2 dataset, our method improves the adversarial accuracy over the best existing defense approach by more than 4% with a smaller decrease in task accuracy (0.5% vs 2.5%). Moreover, we show that ATINTER generalizes across multiple downstream tasks and classifiers without having to explicitly retrain it for those settings. Specifically, we find that when ATINTER is trained to remove adversarial perturbations for the sentiment classification task on the SST-2 dataset, it even transfers to a semantically different task of news classification (on AGNews) and improves the adversarial robustness by more than 10%.

Cascaded Gaps: Towards Gap-Dependent Regret for Risk-Sensitive Reinforcement Learning

In this paper, we study gap-dependent regret guarantees for risk-sensitive reinforcement learning based on the entropic risk measure. We propose a novel definition of sub-optimality gaps, which we call cascaded gaps, and we discuss their key components that adapt to the underlying structures of the problem. Based on the cascaded gaps, we derive non-asymptotic and logarithmic regret bounds for two model-free algorithms under episodic Markov decision processes. We show that, in appropriate settings, these bounds feature exponential improvement over existing ones that are independent of gaps. We also prove gap-dependent lower bounds, which certify the near optimality of the upper bounds.

Exponential Bellman Equation and Improved Regret Bounds for Risk-Sensitive Reinforcement Learning

We study risk-sensitive reinforcement learning (RL) based on the entropic risk measure. Although existing works have established non-asymptotic regret guarantees for this problem, they leave open an exponential gap between the upper and lower bounds. We identify the deficiencies in existing algorithms and their analysis that result in such a gap. To remedy these deficiencies, we investigate a simple transformation of the risk-sensitive Bellman equations, which we call the exponential Bellman equation. The exponential Bellman equation inspires us to develop a novel analysis of Bellman backup procedures in risk-sensitive RL algorithms, and further motivates the design of a novel exploration mechanism. We show that these analytic and algorithmic innovations together lead to improved regret upper bounds over existing ones.

Dynamic Regret of Policy Optimization in Non-stationary Environments

We consider reinforcement learning (RL) in episodic MDPs with adversarial full-information reward feedback and unknown fixed transition kernels. We propose two model-free policy optimization algorithms, POWER and POWER++, and establish guarantees for their dynamic regret. Compared with the classical notion of static regret, dynamic regret is a stronger notion as it explicitly accounts for the non-stationarity of environments. The dynamic regret attained by the proposed algorithms interpolates between different regimes of non-stationarity, and moreover satisfies a notion of adaptive (near-)optimality, in the sense that it matches the (near-)optimal static regret under slow-changing environments. The dynamic regret bound features two components, one arising from exploration, which deals with the uncertainty of transition kernels, and the other arising from adaptation, which deals with non-stationary environments. Specifically, we show that POWER++ improves over POWER on the second component of the dynamic regret by actively adapting to non-stationarity through prediction. To the best of our knowledge, our work is the first dynamic regret analysis of model-free RL algorithms in non-stationary environments.

Risk-Sensitive Reinforcement Learning: Near-Optimal Risk-Sample Tradeoff in Regret

We study risk-sensitive reinforcement learning in episodic Markov decision processes with unknown transition kernels, where the goal is to optimize the total reward under the risk measure of exponential utility. We propose two provably efficient model-free algorithms, Risk-Sensitive Value Iteration (RSVI) and Risk-Sensitive Q-learning (RSQ). These algorithms implement a form of risk-sensitive optimism in the face of uncertainty, which adapts to both risk-seeking and risk-averse modes of exploration. We prove that RSVI attains an $\tilde{O}\big(\lambda(|\beta| H^2) \cdot \sqrt{H^{3} S^{2}AT} \big)$ regret, while RSQ attains an $\tilde{O}\big(\lambda(|\beta| H^2) \cdot \sqrt{H^{4} SAT} \big)$ regret, where $\lambda(u) = (e^{3u}-1)/u$ for $u>0$. In the above, $\beta$ is the risk parameter of the exponential utility function, $S$ the number of states, $A$ the number of actions, $T$ the total number of timesteps, and $H$ the episode length. On the flip side, we establish a regret lower bound showing that the exponential dependence on $|\beta|$ and $H$ is unavoidable for any algorithm with an $\tilde{O}(\sqrt{T})$ regret (even when the risk objective is on the same scale as the original reward), thus certifying the near-optimality of the proposed algorithms. Our results demonstrate that incorporating risk awareness into reinforcement learning necessitates an exponential cost in $|\beta|$ and $H$, which quantifies the fundamental tradeoff between risk sensitivity (related to aleatoric uncertainty) and sample efficiency (related to epistemic uncertainty). To the best of our knowledge, this is the first regret analysis of risk-sensitive reinforcement learning with the exponential utility.

Achieving the Bayes Error Rate in Synchronization and Block Models by SDP, Robustly

We study the statistical performance of semidefinite programming (SDP) relaxations for clustering under random graph models. Under the $\mathbb{Z}_{2}$ Synchronization model, Censored Block Model and Stochastic Block Model, we show that SDP achieves an error rate of the form \[ \exp\Big[-\big(1-o(1)\big)\bar{n} I^* \Big]. \] Here $\bar{n}$ is an appropriate multiple of the number of nodes and $I^*$ is an information-theoretic measure of the signal-to-noise ratio. We provide matching lower bounds on the Bayes error for each model and therefore demonstrate that the SDP approach is Bayes optimal. As a corollary, our results imply that SDP achieves the optimal exact recovery threshold under each model. Furthermore, we show that SDP is robust: the above bound remains valid under semirandom versions of the models in which the observed graph is modified by a monotone adversary. Our proof is based on a novel primal-dual analysis of SDP under a unified framework for all three models, and the analysis shows that SDP tightly approximates a joint majority voting procedure.

Hidden Integrality of SDP Relaxation for Sub-Gaussian Mixture Models

We consider the problem of estimating the discrete clustering structures under Sub-Gaussian Mixture Models. Our main results establish a hidden integrality property of a semidefinite programming (SDP) relaxation for this problem: while the optimal solutions to the SDP are not integer-valued in general, their estimation errors can be upper bounded in terms of the error of an idealized integer program. The error of the integer program, and hence that of the SDP, are further shown to decay exponentially in the signal-to-noise ratio. To the best of our knowledge, this is the first exponentially decaying error bound for convex relaxations of mixture models, and our results reveal the "global-to-local" mechanism that drives the performance of the SDP relaxation. A corollary of our results shows that in certain regimes the SDP solutions are in fact integral and exact, improving on existing exact recovery results for convex relaxations. More generally, our results establish sufficient conditions for the SDP to correctly recover the cluster memberships of $(1-\delta)$ fraction of the points for any $\delta\in(0,1)$. As a special case, we show that under the $d$-dimensional Stochastic Ball Model, SDP achieves non-trivial (sometimes exact) recovery when the center separation is as small as $\sqrt{1/d}$, which complements previous exact recovery results that require constant separation.

Exponential error rates of SDP for block models: Beyond Grothendieck's inequality

In this paper we consider the cluster estimation problem under the Stochastic Block Model. We show that the semidefinite programming (SDP) formulation for this problem achieves an error rate that decays exponentially in the signal-to-noise ratio. The error bound implies weak recovery in the sparse graph regime with bounded expected degrees, as well as exact recovery in the dense regime. An immediate corollary of our results yields error bounds under the Censored Block Model. Moreover, these error bounds are robust, continuing to hold under heterogeneous edge probabilities and a form of the so-called monotone attack. Significantly, this error rate is achieved by the SDP solution itself without any further pre- or post-processing, and improves upon existing polynomially-decaying error bounds proved using the Grothendieck\textquoteright s inequality. Our analysis has two key ingredients: (i) showing that the graph has a well-behaved spectrum, even in the sparse regime, after discounting an exponentially small number of edges, and (ii) an order-statistics argument that governs the final error rate. Both arguments highlight the implicit regularization effect of the SDP formulation.