Personalized Graph Federated Learning with Differential Privacy

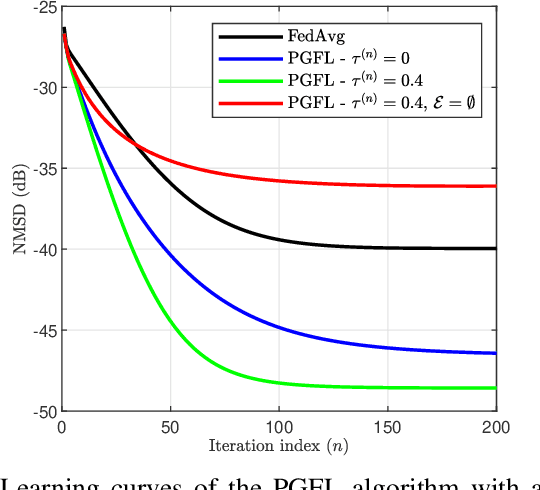
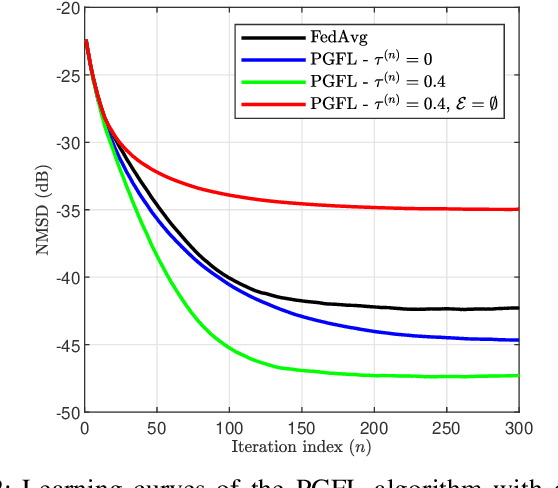
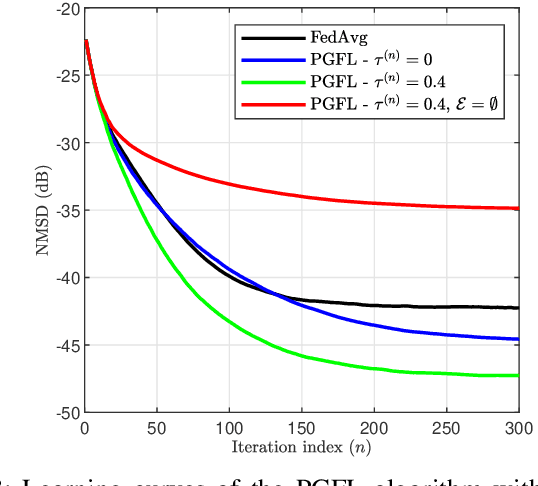
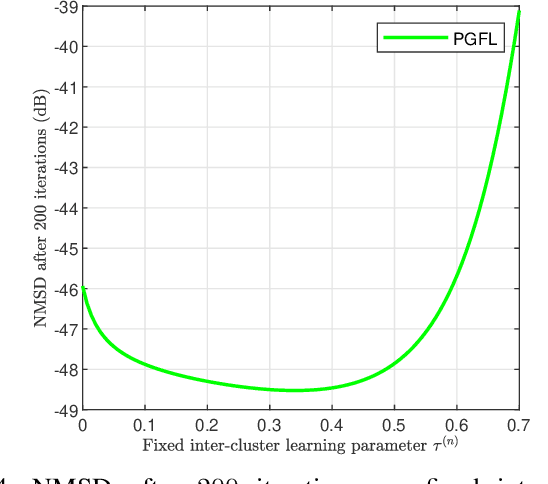
This paper presents a personalized graph federated learning (PGFL) framework in which distributedly connected servers and their respective edge devices collaboratively learn device or cluster-specific models while maintaining the privacy of every individual device. The proposed approach exploits similarities among different models to provide a more relevant experience for each device, even in situations with diverse data distributions and disproportionate datasets. Furthermore, to ensure a secure and efficient approach to collaborative personalized learning, we study a variant of the PGFL implementation that utilizes differential privacy, specifically zero-concentrated differential privacy, where a noise sequence perturbs model exchanges. Our mathematical analysis shows that the proposed privacy-preserving PGFL algorithm converges to the optimal cluster-specific solution for each cluster in linear time. It also shows that exploiting similarities among clusters leads to an alternative output whose distance to the original solution is bounded, and that this bound can be adjusted by modifying the algorithm's hyperparameters. Further, our analysis shows that the algorithm ensures local differential privacy for all clients in terms of zero-concentrated differential privacy. Finally, the performance of the proposed PGFL algorithm is examined by performing numerical experiments in the context of regression and classification using synthetic data and the MNIST dataset.

Asynchronous Online Federated Learning with Reduced Communication Requirements

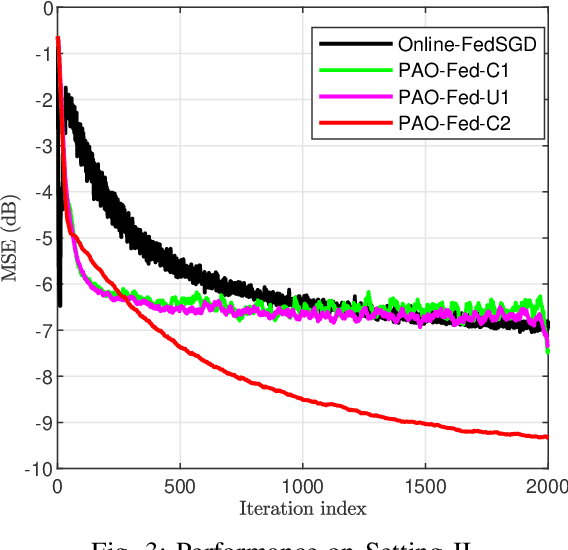
Online federated learning (FL) enables geographically distributed devices to learn a global shared model from locally available streaming data. Most online FL literature considers a best-case scenario regarding the participating clients and the communication channels. However, these assumptions are often not met in real-world applications. Asynchronous settings can reflect a more realistic environment, such as heterogeneous client participation due to available computational power and battery constraints, as well as delays caused by communication channels or straggler devices. Further, in most applications, energy efficiency must be taken into consideration. Using the principles of partial-sharing-based communications, we propose a communication-efficient asynchronous online federated learning (PAO-Fed) strategy. By reducing the communication overhead of the participants, the proposed method renders participation in the learning task more accessible and efficient. In addition, the proposed aggregation mechanism accounts for random participation, handles delayed updates and mitigates their effect on accuracy. We prove the first and second-order convergence of the proposed PAO-Fed method and obtain an expression for its steady-state mean square deviation. Finally, we conduct comprehensive simulations to study the performance of the proposed method on both synthetic and real-life datasets. The simulations reveal that in asynchronous settings, the proposed PAO-Fed is able to achieve the same convergence properties as that of the online federated stochastic gradient while reducing the communication overhead by 98 percent.

Resource-Aware Asynchronous Online Federated Learning for Nonlinear Regression

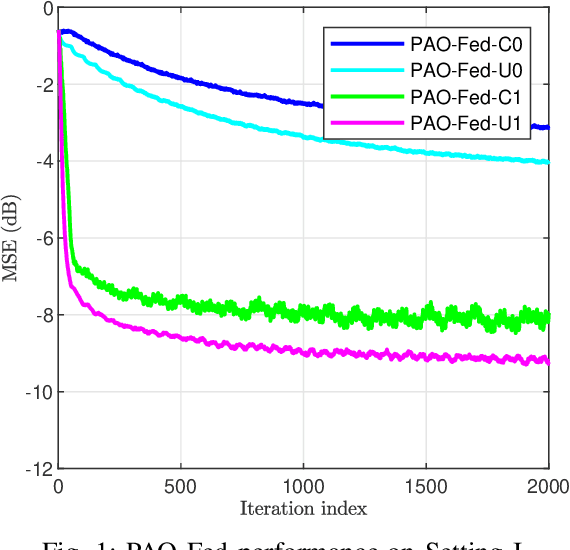
Many assumptions in the federated learning literature present a best-case scenario that can not be satisfied in most real-world applications. An asynchronous setting reflects the realistic environment in which federated learning methods must be able to operate reliably. Besides varying amounts of non-IID data at participants, the asynchronous setting models heterogeneous client participation due to available computational power and battery constraints and also accounts for delayed communications between clients and the server. To reduce the communication overhead associated with asynchronous online federated learning (ASO-Fed), we use the principles of partial-sharing-based communication. In this manner, we reduce the communication load of the participants and, therefore, render participation in the learning task more accessible. We prove the convergence of the proposed ASO-Fed and provide simulations to analyze its behavior further. The simulations reveal that, in the asynchronous setting, it is possible to achieve the same convergence as the federated stochastic gradient (Online-FedSGD) while reducing the communication tenfold.

Communication-Efficient Online Federated Learning Framework for Nonlinear Regression

Federated learning (FL) literature typically assumes that each client has a fixed amount of data, which is unrealistic in many practical applications. Some recent works introduced a framework for online FL (Online-Fed) wherein clients perform model learning on streaming data and communicate the model to the server; however, they do not address the associated communication overhead. As a solution, this paper presents a partial-sharing-based online federated learning framework (PSO-Fed) that enables clients to update their local models using continuous streaming data and share only portions of those updated models with the server. During a global iteration of PSO-Fed, non-participant clients have the privilege to update their local models with new data. Here, we consider a global task of kernel regression, where clients use a random Fourier features-based kernel LMS on their data for local learning. We examine the mean convergence of the PSO-Fed for kernel regression. Experimental results show that PSO-Fed can achieve competitive performance with a significantly lower communication overhead than Online-Fed.

On Stability and Convergence of Distributed Filters

Recent years have bore witness to the proliferation of distributed filtering techniques, where a collection of agents communicating over an ad-hoc network aim to collaboratively estimate and track the state of a system. These techniques form the enabling technology of modern multi-agent systems and have gained great importance in the engineering community. Although most distributed filtering techniques come with a set of stability and convergence criteria, the conditions imposed are found to be unnecessarily restrictive. The paradigm of stability and convergence in distributed filtering is revised in this manuscript. Accordingly, a general distributed filter is constructed and its estimation error dynamics is formulated. The conducted analysis demonstrates that conditions for achieving stable filtering operations are the same as those required in the centralized filtering setting. Finally, the concepts are demonstrated in a Kalman filtering framework and validated using simulation examples.

Analysis of a Reduced-Communication Diffusion LMS Algorithm

In diffusion-based algorithms for adaptive distributed estimation, each node of an adaptive network estimates a target parameter vector by creating an intermediate estimate and then combining the intermediate estimates available within its closed neighborhood. We analyze the performance of a reduced-communication diffusion least mean-square (RC-DLMS) algorithm, which allows each node to receive the intermediate estimates of only a subset of its neighbors at each iteration. This algorithm eases the usage of network communication resources and delivers a trade-off between estimation performance and communication cost. We show analytically that the RC-DLMS algorithm is stable and convergent in both mean and mean-square senses. We also calculate its theoretical steady-state mean-square deviation. Simulation results demonstrate a good match between theory and experiment.