Alpha Mining and Enhancing via Warm Start Genetic Programming for Quantitative Investment

Traditional genetic programming (GP) often struggles in stock alpha factor discovery due to its vast search space, overwhelming computational burden, and sporadic effective alphas. We find that GP performs better when focusing on promising regions rather than random searching. This paper proposes a new GP framework with carefully chosen initialization and structural constraints to enhance search performance and improve the interpretability of the alpha factors. This approach is motivated by and mimics the alpha searching practice and aims to boost the efficiency of such a process. Analysis of 2020-2024 Chinese stock market data shows that our method yields superior out-of-sample prediction results and higher portfolio returns than the benchmark.

Sparsified Simultaneous Confidence Intervals for High-Dimensional Linear Models

Statistical inference of the high-dimensional regression coefficients is challenging because the uncertainty introduced by the model selection procedure is hard to account for. A critical question remains unsettled; that is, is it possible and how to embed the inference of the model into the simultaneous inference of the coefficients? To this end, we propose a notion of simultaneous confidence intervals called the sparsified simultaneous confidence intervals. Our intervals are sparse in the sense that some of the intervals' upper and lower bounds are shrunken to zero (i.e., $[0,0]$), indicating the unimportance of the corresponding covariates. These covariates should be excluded from the final model. The rest of the intervals, either containing zero (e.g., $[-1,1]$ or $[0,1]$) or not containing zero (e.g., $[2,3]$), indicate the plausible and significant covariates, respectively. The proposed method can be coupled with various selection procedures, making it ideal for comparing their uncertainty. For the proposed method, we establish desirable asymptotic properties, develop intuitive graphical tools for visualization, and justify its superior performance through simulation and real data analysis.

Statistical inference on random dot product graphs: a survey

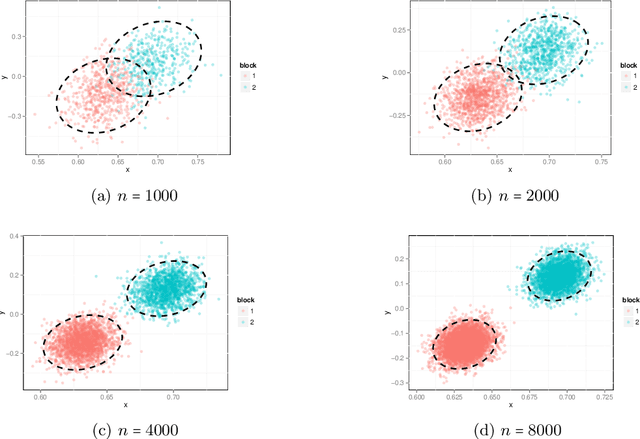
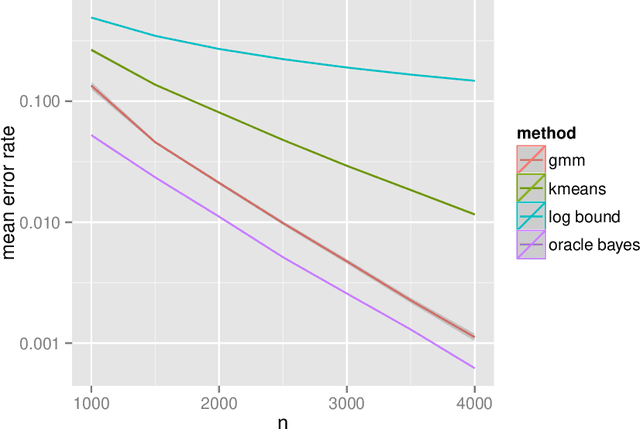
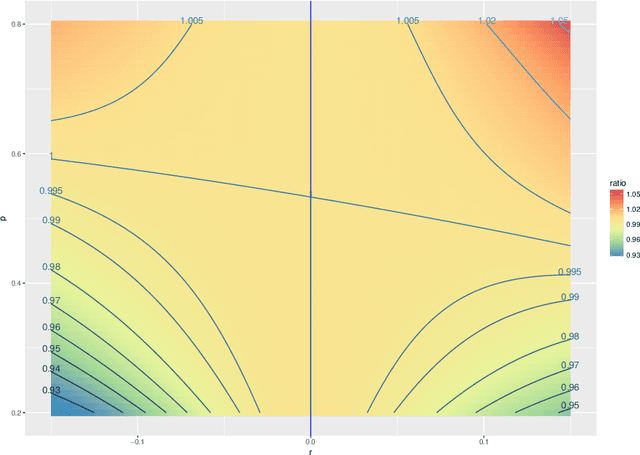
The random dot product graph (RDPG) is an independent-edge random graph that is analytically tractable and, simultaneously, either encompasses or can successfully approximate a wide range of random graphs, from relatively simple stochastic block models to complex latent position graphs. In this survey paper, we describe a comprehensive paradigm for statistical inference on random dot product graphs, a paradigm centered on spectral embeddings of adjacency and Laplacian matrices. We examine the analogues, in graph inference, of several canonical tenets of classical Euclidean inference: in particular, we summarize a body of existing results on the consistency and asymptotic normality of the adjacency and Laplacian spectral embeddings, and the role these spectral embeddings can play in the construction of single- and multi-sample hypothesis tests for graph data. We investigate several real-world applications, including community detection and classification in large social networks and the determination of functional and biologically relevant network properties from an exploratory data analysis of the Drosophila connectome. We outline requisite background and current open problems in spectral graph inference.

Semiparametric spectral modeling of the Drosophila connectome

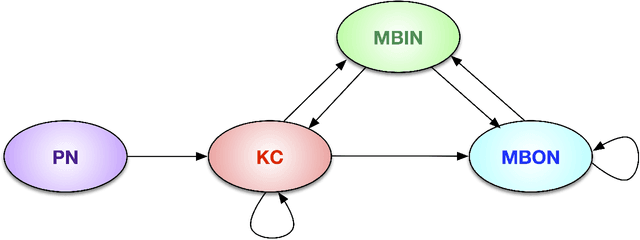
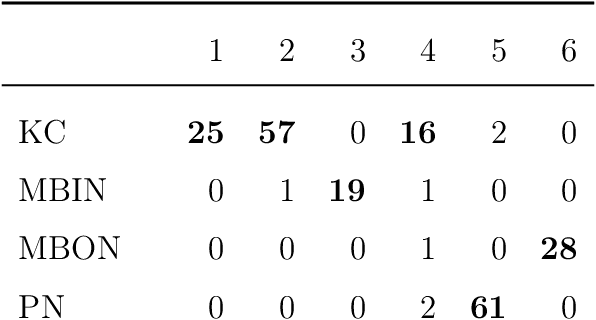
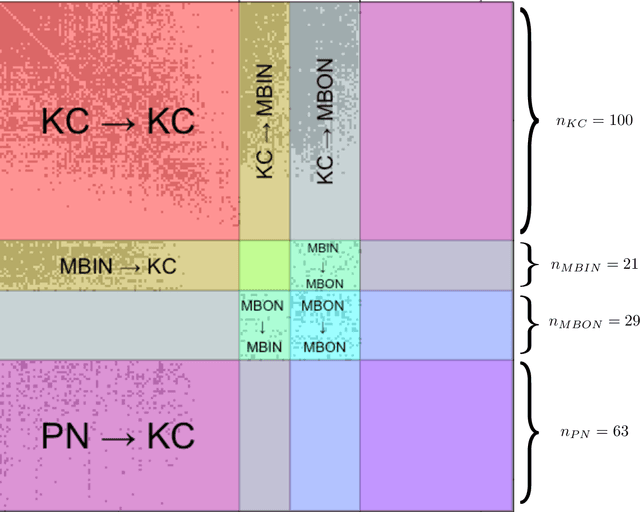
We present semiparametric spectral modeling of the complete larval Drosophila mushroom body connectome. Motivated by a thorough exploratory data analysis of the network via Gaussian mixture modeling (GMM) in the adjacency spectral embedding (ASE) representation space, we introduce the latent structure model (LSM) for network modeling and inference. LSM is a generalization of the stochastic block model (SBM) and a special case of the random dot product graph (RDPG) latent position model, and is amenable to semiparametric GMM in the ASE representation space. The resulting connectome code derived via semiparametric GMM composed with ASE captures latent connectome structure and elucidates biologically relevant neuronal properties.