Learning to rank via combining representations

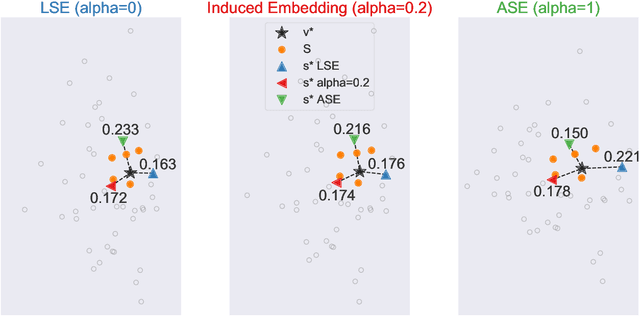
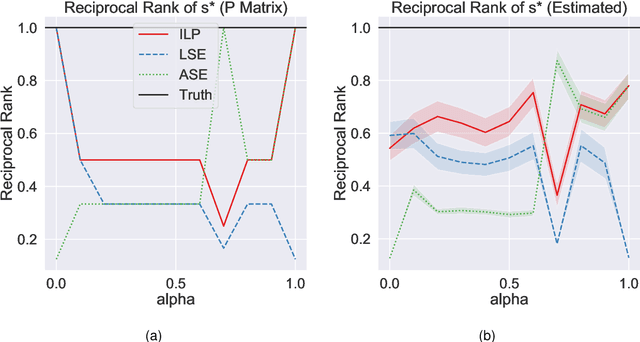
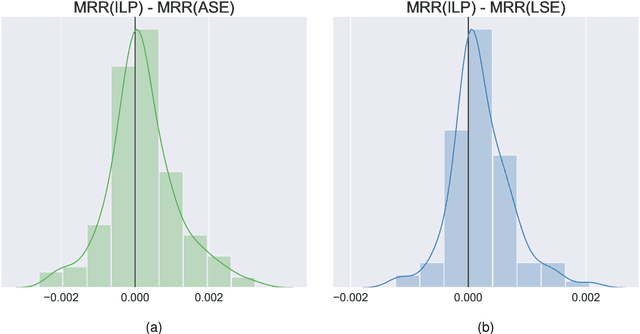
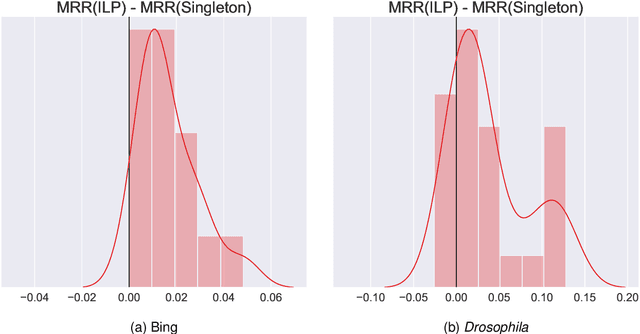
Learning to rank -- producing a ranked list of items specific to a query and with respect to a set of supervisory items -- is a problem of general interest. The setting we consider is one in which no analytic description of what constitutes a good ranking is available. Instead, we have a collection of representations and supervisory information consisting of a (target item, interesting items set) pair. We demonstrate -- analytically, in simulation, and in real data examples -- that learning to rank via combining representations using an integer linear program is effective when the supervision is as light as "these few items are similar to your item of interest." While this nomination task is of general interest, for specificity we present our methodology from the perspective of vertex nomination in graphs. The methodology described herein is model agnostic.

Semiparametric spectral modeling of the Drosophila connectome

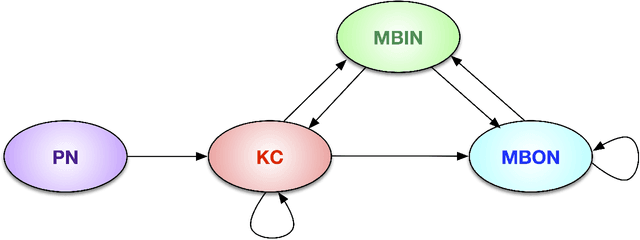
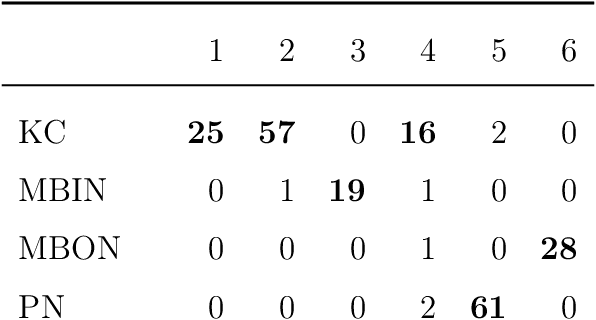
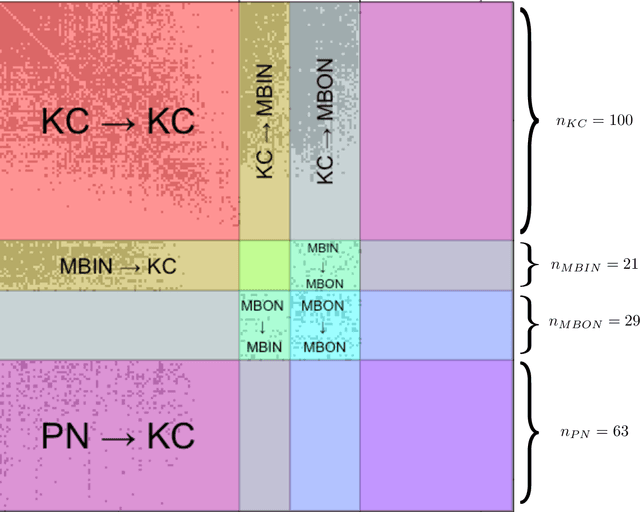
We present semiparametric spectral modeling of the complete larval Drosophila mushroom body connectome. Motivated by a thorough exploratory data analysis of the network via Gaussian mixture modeling (GMM) in the adjacency spectral embedding (ASE) representation space, we introduce the latent structure model (LSM) for network modeling and inference. LSM is a generalization of the stochastic block model (SBM) and a special case of the random dot product graph (RDPG) latent position model, and is amenable to semiparametric GMM in the ASE representation space. The resulting connectome code derived via semiparametric GMM composed with ASE captures latent connectome structure and elucidates biologically relevant neuronal properties.