CaveAgent: Transforming LLMs into Stateful Runtime Operators

LLM-based agents are increasingly capable of complex task execution, yet current agentic systems remain constrained by text-centric paradigms. Traditional approaches rely on procedural JSON-based function calling, which often struggles with long-horizon tasks due to fragile multi-turn dependencies and context drift. In this paper, we present CaveAgent, a framework that transforms the paradigm from "LLM-as-Text-Generator" to "LLM-as-Runtime-Operator." We introduce a Dual-stream Context Architecture that decouples state management into a lightweight semantic stream for reasoning and a persistent, deterministic Python Runtime stream for execution. In addition to leveraging code generation to efficiently resolve interdependent sub-tasks (e.g., loops, conditionals) in a single step, we introduce \textit{Stateful Runtime Management} in CaveAgent. Distinct from existing code-based approaches that remain text-bound and lack the support for external object injection and retrieval, CaveAgent injects, manipulates, and retrieves complex Python objects (e.g., DataFrames, database connections) that persist across turns. This persistence mechanism acts as a high-fidelity external memory to eliminate context drift, avoid catastrophic forgetting, while ensuring that processed data flows losslessly to downstream applications. Comprehensive evaluations on Tau$^2$-bench, BFCL and various case studies across representative SOTA LLMs demonstrate CaveAgent's superiority. Specifically, our framework achieves a 10.5\% success rate improvement on retail tasks and reduces total token consumption by 28.4\% in multi-turn scenarios. On data-intensive tasks, direct variable storage and retrieval reduces token consumption by 59\%, allowing CaveAgent to handle large-scale data that causes context overflow failures in both JSON-based and Code-based agents.

Improving Adversarial Robustness via Phase and Amplitude-aware Prompting

Deep neural networks are found to be vulnerable to adversarial noises. The prompt-based defense has been increasingly studied due to its high efficiency. However, existing prompt-based defenses mainly exploited mixed prompt patterns, where critical patterns closely related to object semantics lack sufficient focus. The phase and amplitude spectra have been proven to be highly related to specific semantic patterns and crucial for robustness. To this end, in this paper, we propose a Phase and Amplitude-aware Prompting (PAP) defense. Specifically, we construct phase-level and amplitude-level prompts for each class, and adjust weights for prompting according to the model's robust performance under these prompts during training. During testing, we select prompts for each image using its predicted label to obtain the prompted image, which is inputted to the model to get the final prediction. Experimental results demonstrate the effectiveness of our method.

On-the-Fly SfM: What you capture is What you get

Over the last decades, ample achievements have been made on Structure from motion (SfM). However, the vast majority of them basically work in an offline manner, i.e., images are firstly captured and then fed together into a SfM pipeline for obtaining poses and sparse point cloud. In this work, on the contrary, we present an on-the-fly SfM: running online SfM while image capturing, the newly taken On-the-Fly image is online estimated with the corresponding pose and points, i.e., what you capture is what you get. Specifically, our approach firstly employs a vocabulary tree that is unsupervised trained using learning-based global features for fast image retrieval of newly fly-in image. Then, a robust feature matching mechanism with least squares (LSM) is presented to improve image registration performance. Finally, via investigating the influence of newly fly-in image's connected neighboring images, an efficient hierarchical weighted local bundle adjustment (BA) is used for optimization. Extensive experimental results demonstrate that on-the-fly SfM can meet the goal of robustly registering the images while capturing in an online way.

Katyusha Acceleration for Convex Finite-Sum Compositional Optimization

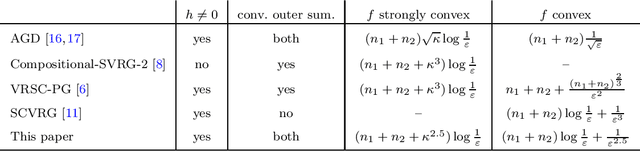
Structured problems arise in many applications. To solve these problems, it is important to leverage the structure information. This paper focuses on convex problems with a finite-sum compositional structure. Finite-sum problems appear as the sample average approximation of a stochastic optimization problem and also arise in machine learning with a huge amount of training data. One popularly used numerical approach for finite-sum problems is the stochastic gradient method (SGM). However, the additional compositional structure prohibits easy access to unbiased stochastic approximation of the gradient, so directly applying the SGM to a finite-sum compositional optimization problem (COP) is often inefficient. We design new algorithms for solving strongly-convex and also convex two-level finite-sum COPs. Our design incorporates the Katyusha acceleration technique and adopts the mini-batch sampling from both outer-level and inner-level finite-sum. We first analyze the algorithm for strongly-convex finite-sum COPs. Similar to a few existing works, we obtain linear convergence rate in terms of the expected objective error, and from the convergence rate result, we then establish complexity results of the algorithm to produce an $\varepsilon$-solution. Our complexity results have the same dependence on the number of component functions as existing works. However, due to the use of Katyusha acceleration, our results have better dependence on the condition number $\kappa$ and improve to $\kappa^{2.5}$ from the best-known $\kappa^3$. Finally, we analyze the algorithm for convex finite-sum COPs, which uses as a subroutine the algorithm for strongly-convex finite-sum COPs. Again, we obtain better complexity results than existing works in terms of the dependence on $\varepsilon$, improving to $\varepsilon^{-2.5}$ from the best-known $\varepsilon^{-3}$.

Compressed domain image classification using a multi-rate neural network

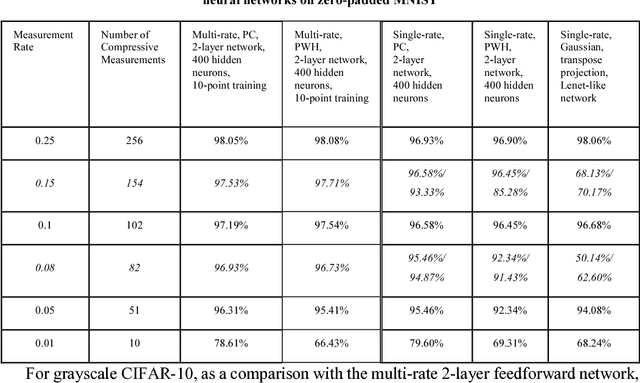
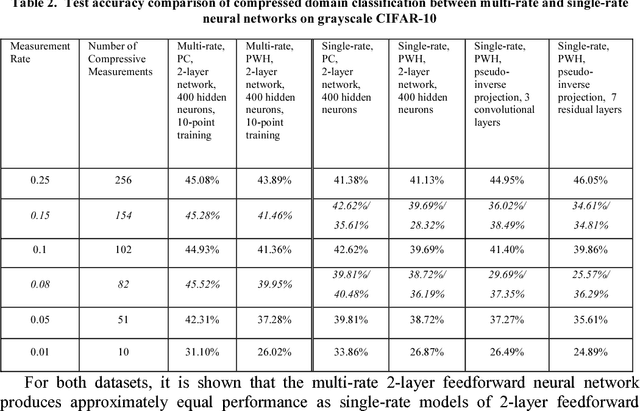
Compressed domain image classification aims to directly perform classification on compressive measurements generated from the single-pixel camera. While neural network approaches have achieved state-of-the-art performance, previous methods require training a dedicated network for each different measurement rate which is computationally costly. In this work, we present a general approach that endows a single neural network with multi-rate property for compressed domain classification where a single network is capable of classifying over an arbitrary number of measurements using dataset-independent fixed binary sensing patterns. We demonstrate the multi-rate neural network performance on MNIST and grayscale CIFAR-10 datasets. We also show that using the Partial Complete binary sensing matrix, the multi-rate network outperforms previous methods especially in the case of very few measurements.