Understand the Effectiveness of Shortcuts through the Lens of DCA

Difference-of-Convex Algorithm (DCA) is a well-known nonconvex optimization algorithm for minimizing a nonconvex function that can be expressed as the difference of two convex ones. Many famous existing optimization algorithms, such as SGD and proximal point methods, can be viewed as special DCAs with specific DC decompositions, making it a powerful framework for optimization. On the other hand, shortcuts are a key architectural feature in modern deep neural networks, facilitating both training and optimization. We showed that the shortcut neural network gradient can be obtained by applying DCA to vanilla neural networks, networks without shortcut connections. Therefore, from the perspective of DCA, we can better understand the effectiveness of networks with shortcuts. Moreover, we proposed a new architecture called NegNet that does not fit the previous interpretation but performs on par with ResNet and can be included in the DCA framework.

A Refined Inertial DCA for DC Programming

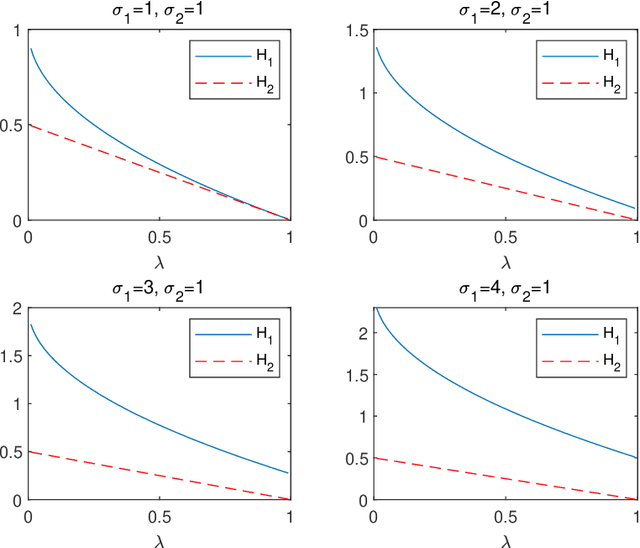
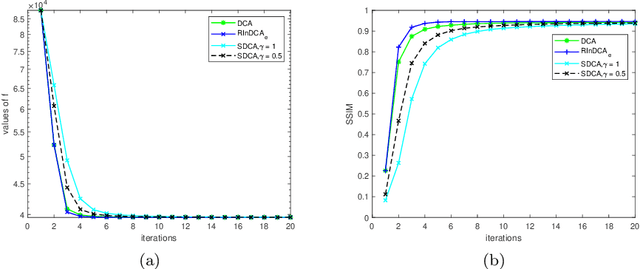
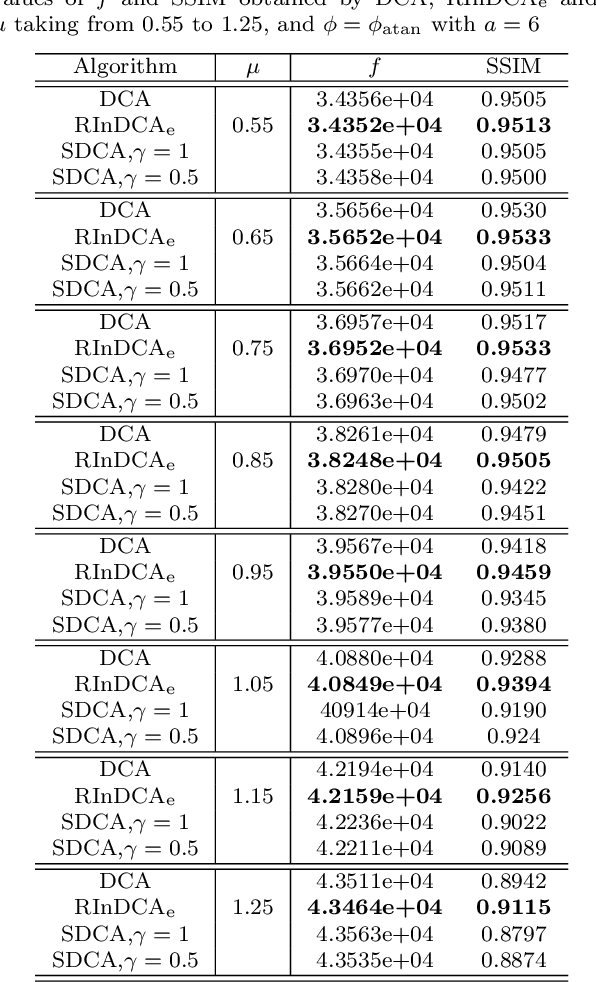
We consider the difference-of-convex (DC) programming problems whose objective function is level-bounded. The classical DC algorithm (DCA) is well-known for solving this kind of problems, which returns a critical point. Recently, de Oliveira and Tcheo incorporated the inertial-force procedure into DCA (InDCA) for potential acceleration and preventing the algorithm from converging to a critical point which is not d(directional)-stationary. In this paper, based on InDCA, we propose two refined inertial DCA (RInDCA) with enlarged inertial step-sizes for better acceleration. We demonstrate the subsequential convergence of our refined versions to a critical point. In addition, by assuming the Kurdyka-Lojasiewicz (KL) property of the objective function, we establish the sequential convergence of RInDCA. Numerical simulations on image restoration problem show the benefit of enlarged step-size.

Spatio-Temporal Neural Network for Fitting and Forecasting COVID-19

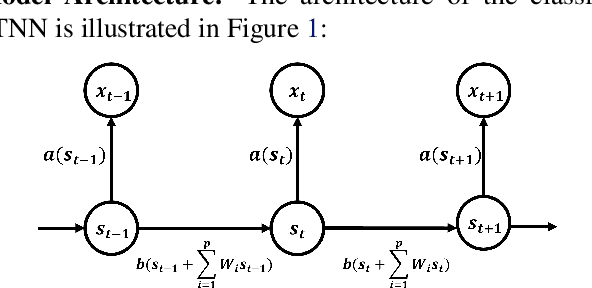
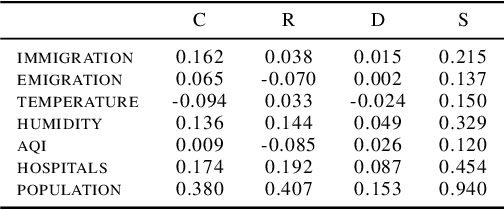
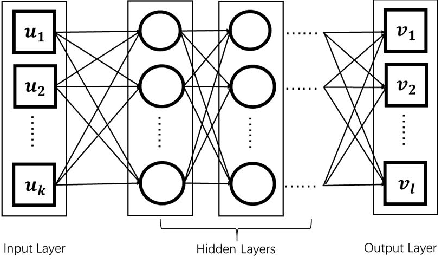
We established a Spatio-Temporal Neural Network, namely STNN, to forecast the spread of the coronavirus COVID-19 outbreak worldwide in 2020. The basic structure of STNN is similar to the Recurrent Neural Network (RNN) incorporating with not only temporal data but also spatial features. Two improved STNN architectures, namely the STNN with Augmented Spatial States (STNN-A) and the STNN with Input Gate (STNN-I), are proposed, which ensure more predictability and flexibility. STNN and its variants can be trained using Stochastic Gradient Descent (SGD) algorithm and its improved variants (e.g., Adam, AdaGrad and RMSProp). Our STNN models are compared with several classical epidemic prediction models, including the fully-connected neural network (BPNN), and the recurrent neural network (RNN), the classical curve fitting models, as well as the SEIR dynamical system model. Numerical simulations demonstrate that STNN models outperform many others by providing more accurate fitting and prediction, and by handling both spatial and temporal data.

A Difference-of-Convex Programming Approach With Parallel Branch-and-Bound For Sentence Compression Via A Hybrid Extractive Model

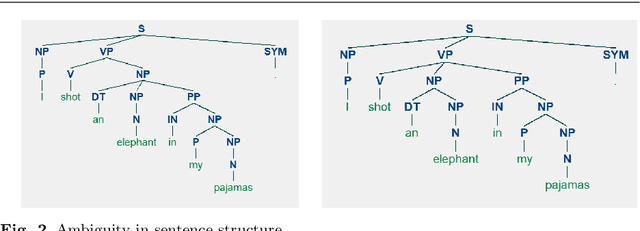
Sentence compression is an important problem in natural language processing with wide applications in text summarization, search engine and human-AI interaction system etc. In this paper, we design a hybrid extractive sentence compression model combining a probability language model and a parse tree language model for compressing sentences by guaranteeing the syntax correctness of the compression results. Our compression model is formulated as an integer linear programming problem, which can be rewritten as a Difference-of-Convex (DC) programming problem based on the exact penalty technique. We use a well known efficient DC algorithm -- DCA to handle the penalized problem for local optimal solutions. Then a hybrid global optimization algorithm combining DCA with a parallel branch-and-bound framework, namely PDCABB, is used for finding global optimal solutions. Numerical results demonstrate that our sentence compression model can provide excellent compression results evaluated by F-score, and indicate that PDCABB is a promising algorithm for solving our sentence compression model.

Sentence Compression via DC Programming Approach

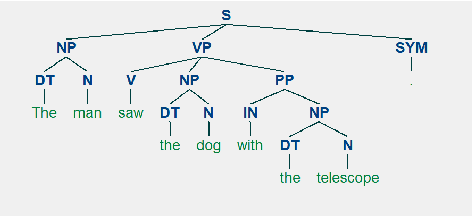
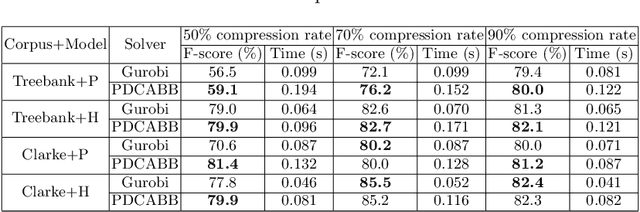
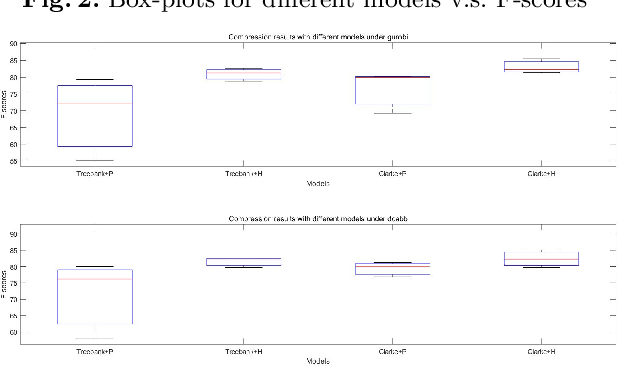
Sentence compression is an important problem in natural language processing. In this paper, we firstly establish a new sentence compression model based on the probability model and the parse tree model. Our sentence compression model is equivalent to an integer linear program (ILP) which can both guarantee the syntax correctness of the compression and save the main meaning. We propose using a DC (Difference of convex) programming approach (DCA) for finding local optimal solution of our model. Combing DCA with a parallel-branch-and-bound framework, we can find global optimal solution. Numerical results demonstrate the good quality of our sentence compression model and the excellent performance of our proposed solution algorithm.