A Refined Inertial DCA for DC Programming
Paper and Code
Apr 30, 2021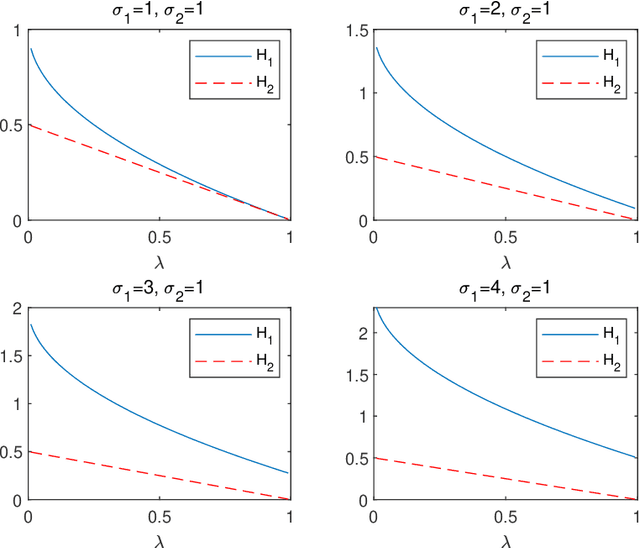

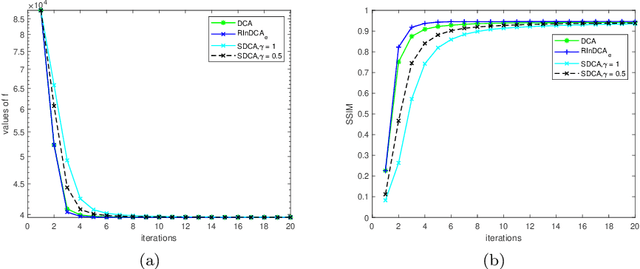
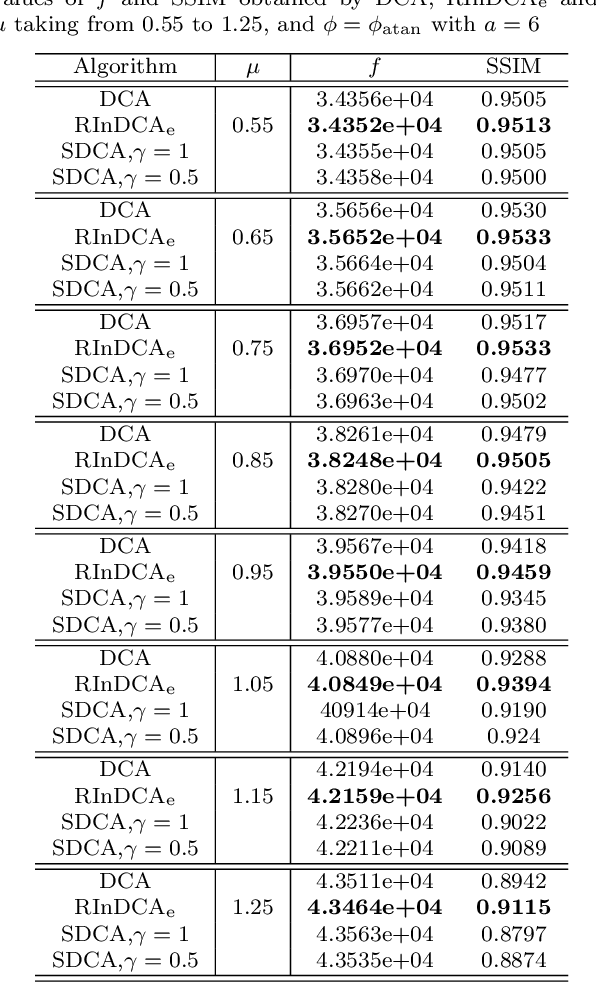
We consider the difference-of-convex (DC) programming problems whose objective function is level-bounded. The classical DC algorithm (DCA) is well-known for solving this kind of problems, which returns a critical point. Recently, de Oliveira and Tcheo incorporated the inertial-force procedure into DCA (InDCA) for potential acceleration and preventing the algorithm from converging to a critical point which is not d(directional)-stationary. In this paper, based on InDCA, we propose two refined inertial DCA (RInDCA) with enlarged inertial step-sizes for better acceleration. We demonstrate the subsequential convergence of our refined versions to a critical point. In addition, by assuming the Kurdyka-Lojasiewicz (KL) property of the objective function, we establish the sequential convergence of RInDCA. Numerical simulations on image restoration problem show the benefit of enlarged step-size.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge