Estimation Beyond Data Reweighting: Kernel Method of Moments

Moment restrictions and their conditional counterparts emerge in many areas of machine learning and statistics ranging from causal inference to reinforcement learning. Estimators for these tasks, generally called methods of moments, include the prominent generalized method of moments (GMM) which has recently gained attention in causal inference. GMM is a special case of the broader family of empirical likelihood estimators which are based on approximating a population distribution by means of minimizing a $\varphi$-divergence to an empirical distribution. However, the use of $\varphi$-divergences effectively limits the candidate distributions to reweightings of the data samples. We lift this long-standing limitation and provide a method of moments that goes beyond data reweighting. This is achieved by defining an empirical likelihood estimator based on maximum mean discrepancy which we term the kernel method of moments (KMM). We provide a variant of our estimator for conditional moment restrictions and show that it is asymptotically first-order optimal for such problems. Finally, we show that our method achieves competitive performance on several conditional moment restriction tasks.

Shallow Representation is Deep: Learning Uncertainty-aware and Worst-case Random Feature Dynamics

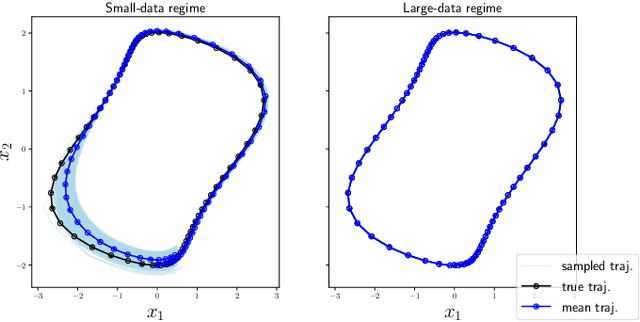
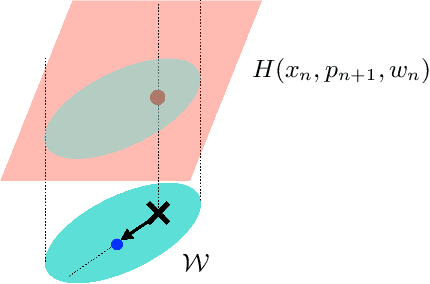
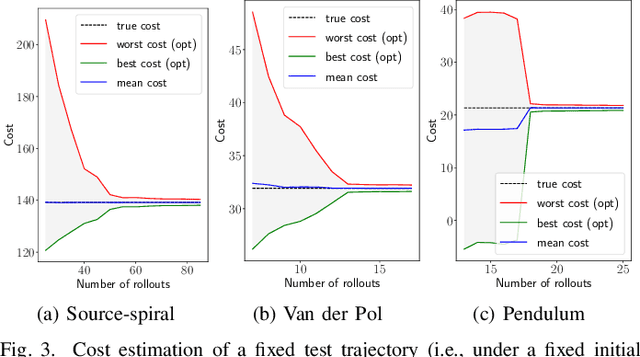
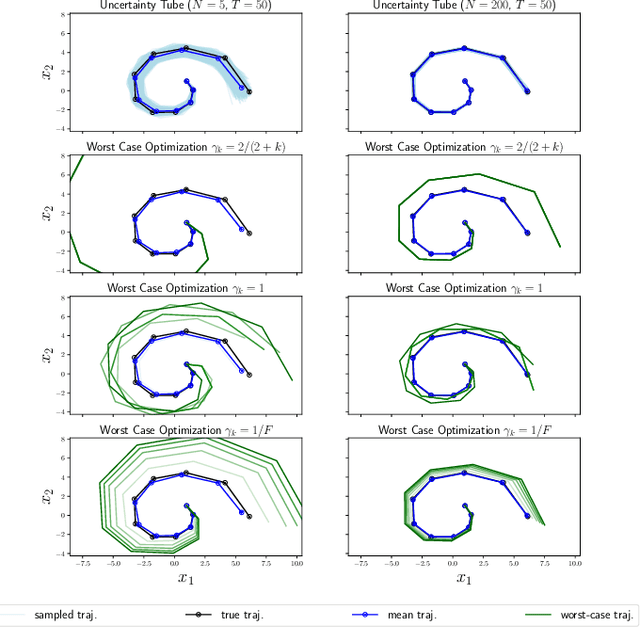
Random features is a powerful universal function approximator that inherits the theoretical rigor of kernel methods and can scale up to modern learning tasks. This paper views uncertain system models as unknown or uncertain smooth functions in universal reproducing kernel Hilbert spaces. By directly approximating the one-step dynamics function using random features with uncertain parameters, which are equivalent to a shallow Bayesian neural network, we then view the whole dynamical system as a multi-layer neural network. Exploiting the structure of Hamiltonian dynamics, we show that finding worst-case dynamics realizations using Pontryagin's minimum principle is equivalent to performing the Frank-Wolfe algorithm on the deep net. Various numerical experiments on dynamics learning showcase the capacity of our modeling methodology.

From Majorization to Interpolation: Distributionally Robust Learning using Kernel Smoothing

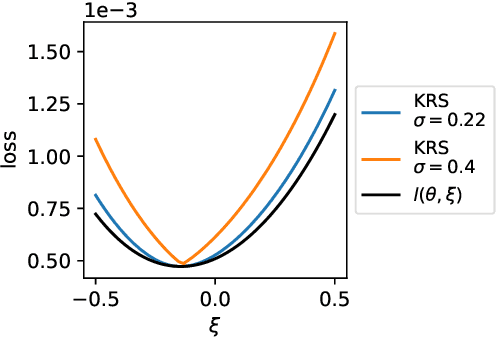
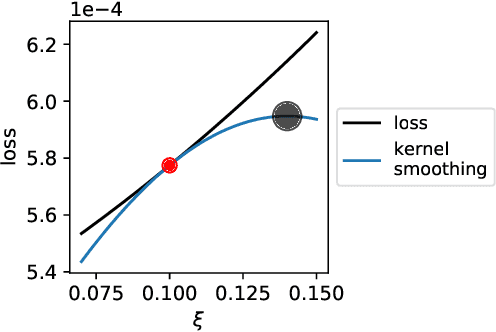
We study the function approximation aspect of distributionally robust optimization (DRO) based on probability metrics, such as the Wasserstein and the maximum mean discrepancy. Our analysis leverages the insight that existing DRO paradigms hinge on function majorants such as the Moreau-Yosida regularization (supremal convolution). Deviating from those, this paper instead proposes robust learning algorithms based on smooth function approximation and interpolation. Our methods are simple in forms and apply to general loss functions without knowing functional norms a priori. Furthermore, we analyze the DRO risk bound decomposition by leveraging smooth function approximators and the convergence rate for empirical kernel mean embedding.

Reliable Real Time Ball Tracking for Robot Table Tennis

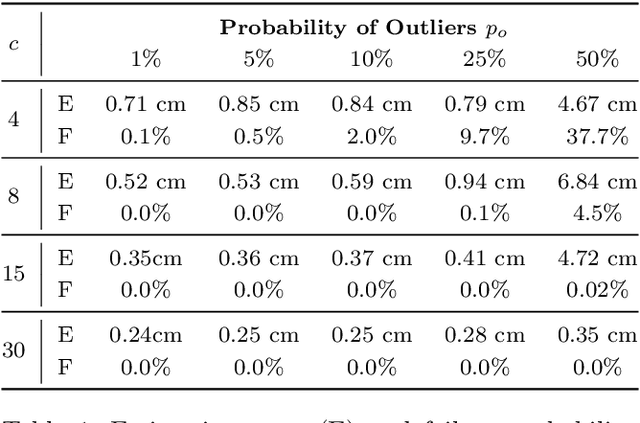
Robot table tennis systems require a vision system that can track the ball position with low latency and high sampling rate. Altering the ball to simplify the tracking using for instance infrared coating changes the physics of the ball trajectory. As a result, table tennis systems use custom tracking systems to track the ball based on heuristic algorithms respecting the real time constrains applied to RGB images captured with a set of cameras. However, these heuristic algorithms often report erroneous ball positions, and the table tennis policies typically need to incorporate additional heuristics to detect and possibly correct outliers. In this paper, we propose a vision system for object detection and tracking that focus on reliability while providing real time performance. Our assumption is that by using multiple cameras, we can find and discard the errors obtained in the object detection phase by checking for consistency with the positions reported by other cameras. We provide an open source implementation of the proposed tracking system to simplify future research in robot table tennis or related tracking applications with strong real time requirements. We evaluate the proposed system thoroughly in simulation and in the real system, outperforming previous work. Furthermore, we show that the accuracy and robustness of the proposed system increases as more cameras are added. Finally, we evaluate the table tennis playing performance of an existing method in the real robot using the proposed vision system. We measure a slight increase in performance compared to a previous vision system even after removing all the heuristics previously present to filter out erroneous ball observations.