Shallow Representation is Deep: Learning Uncertainty-aware and Worst-case Random Feature Dynamics

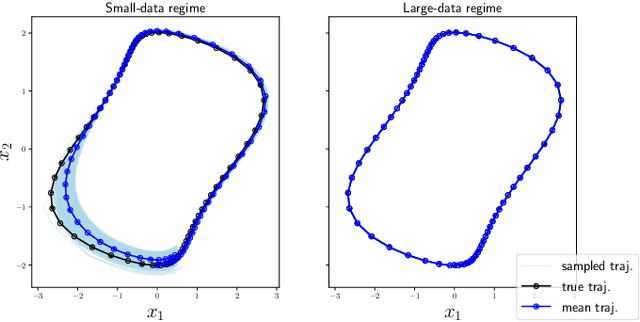
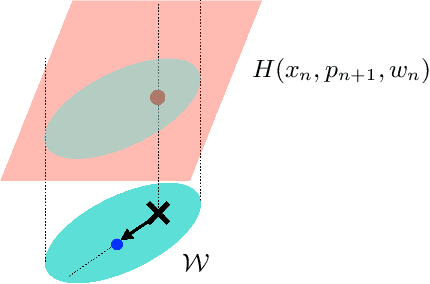
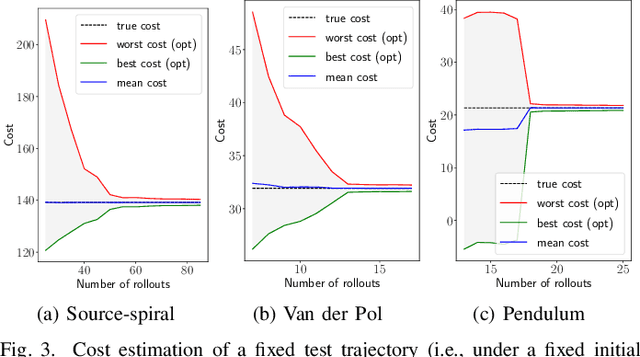
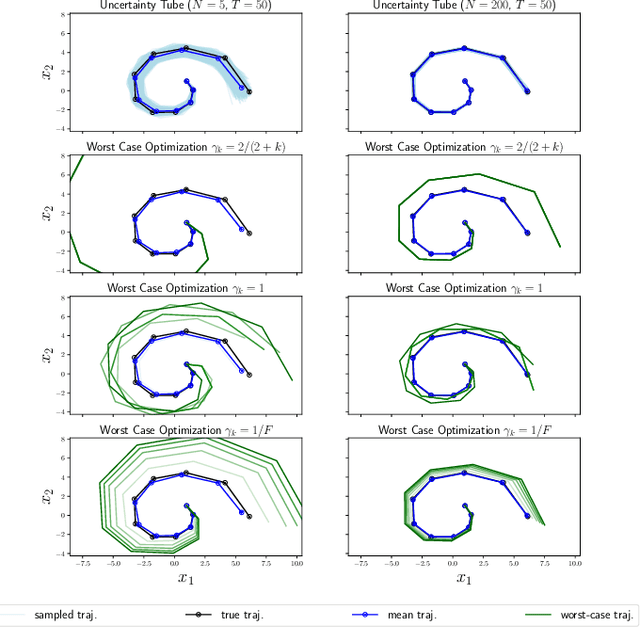
Random features is a powerful universal function approximator that inherits the theoretical rigor of kernel methods and can scale up to modern learning tasks. This paper views uncertain system models as unknown or uncertain smooth functions in universal reproducing kernel Hilbert spaces. By directly approximating the one-step dynamics function using random features with uncertain parameters, which are equivalent to a shallow Bayesian neural network, we then view the whole dynamical system as a multi-layer neural network. Exploiting the structure of Hamiltonian dynamics, we show that finding worst-case dynamics realizations using Pontryagin's minimum principle is equivalent to performing the Frank-Wolfe algorithm on the deep net. Various numerical experiments on dynamics learning showcase the capacity of our modeling methodology.

Bayesian Online Detection and Prediction of Change Points

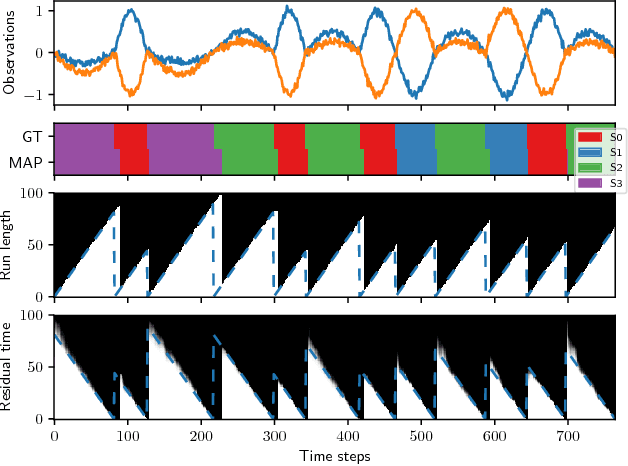
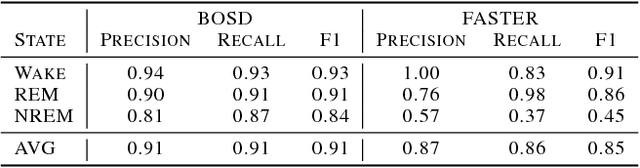
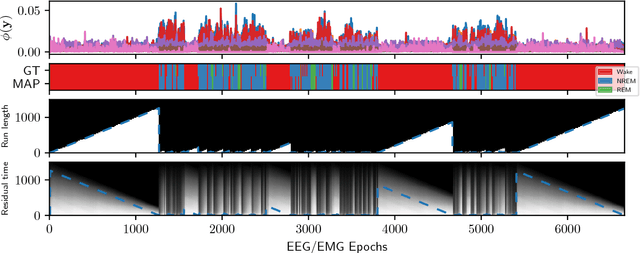
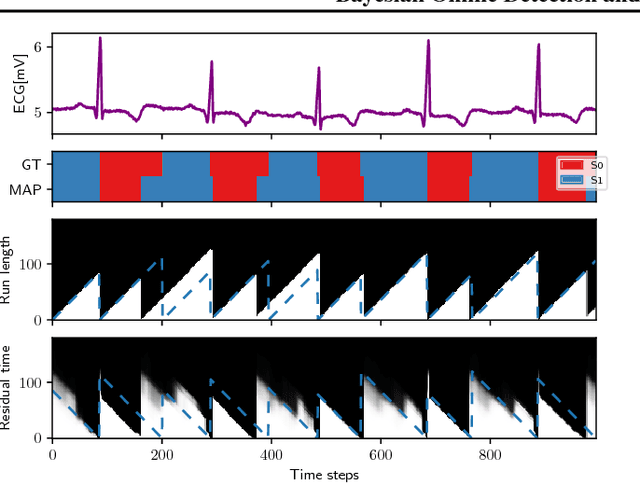
Online detection of instantaneous changes in the generative process of a data sequence generally focuses on retrospective inference of such change points without considering their future occurrences. We extend the Bayesian Online Change Point Detection algorithm to also infer the number of time steps until the next change point (i.e., the residual time). This enables us to handle observation models which depend on the total segment duration, which is useful to model data sequences with temporal scaling. In addition, we extend the model by removing the i.i.d. assumption on the observation model parameters. The resulting inference algorithm for segment detection can be deployed in an online fashion, and we illustrate applications to synthetic and to two medical real-world data sets.