Shallow Representation is Deep: Learning Uncertainty-aware and Worst-case Random Feature Dynamics
Paper and Code
Jun 24, 2021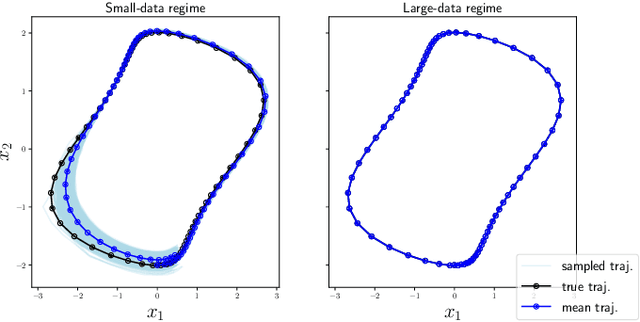
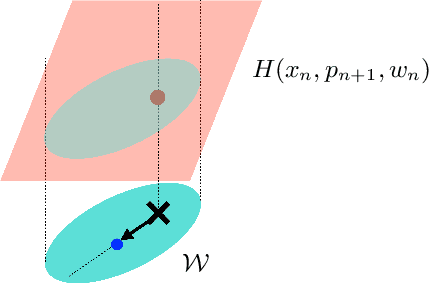
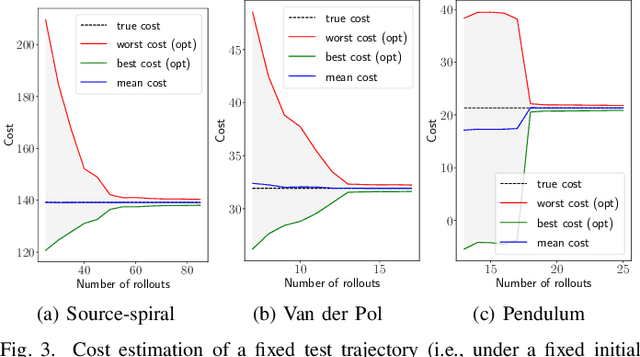
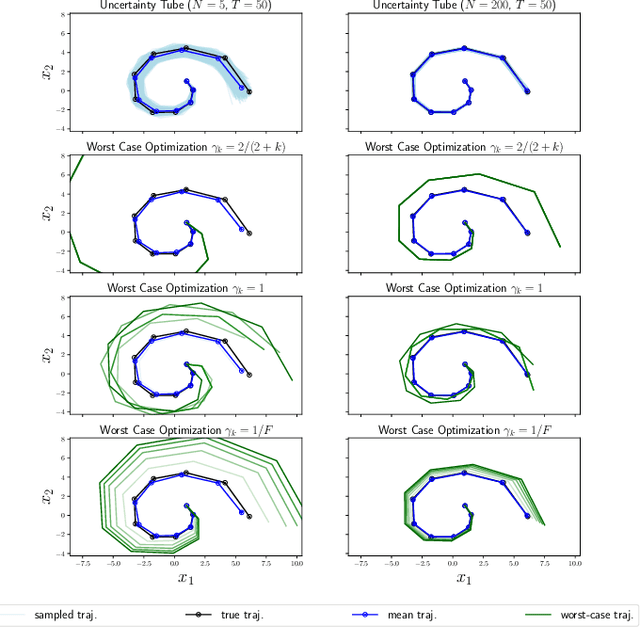
Random features is a powerful universal function approximator that inherits the theoretical rigor of kernel methods and can scale up to modern learning tasks. This paper views uncertain system models as unknown or uncertain smooth functions in universal reproducing kernel Hilbert spaces. By directly approximating the one-step dynamics function using random features with uncertain parameters, which are equivalent to a shallow Bayesian neural network, we then view the whole dynamical system as a multi-layer neural network. Exploiting the structure of Hamiltonian dynamics, we show that finding worst-case dynamics realizations using Pontryagin's minimum principle is equivalent to performing the Frank-Wolfe algorithm on the deep net. Various numerical experiments on dynamics learning showcase the capacity of our modeling methodology.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge