The Basic Geometric Structures of Electromagnetic Digital Information: Statistical characterization of the digital measurement of spatio-Doppler and polarimetric fluctuations of the radar electromagnetic wave

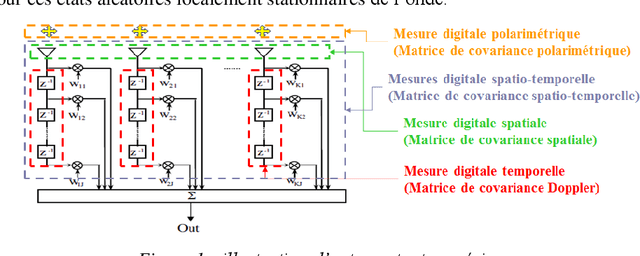
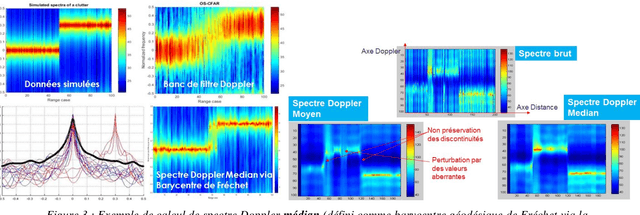
The aim is to describe new geometric approaches to define the statistics of spatio-temporal and polarimetric measurements of the states of an electromagnetic wave, using the works of Maurice Fr{\'e}chet, Jean-Louis Koszul and Jean-Marie Souriau, with in particular the notion of 'average' state of this digital measurement as a Fr{\'e}chet barycentre in a metric space and a model derived from statistical mechanics to define and calculate a maximum density of entropy (extension of the notion of Gaussian) to describe the fluctuations of the electromagnetic wave. The article will illustrate these new tools with examples of radar application for Doppler, spatio-temporal and polarimetric measurement of the electromagnetic wave by introducing a distance on the covariance matrices of the electromagnetic digital signal, based on Fisher's metric from Information Geometry.

Geomstats: A Python Package for Riemannian Geometry in Machine Learning

We introduce Geomstats, an open-source Python toolbox for computations and statistics on nonlinear manifolds, such as hyperbolic spaces, spaces of symmetric positive definite matrices, Lie groups of transformations, and many more. We provide object-oriented and extensively unit-tested implementations. Among others, manifolds come equipped with families of Riemannian metrics, with associated exponential and logarithmic maps, geodesics and parallel transport. Statistics and learning algorithms provide methods for estimation, clustering and dimension reduction on manifolds. All associated operations are vectorized for batch computation and provide support for different execution backends, namely NumPy, PyTorch and TensorFlow, enabling GPU acceleration. This paper presents the package, compares it with related libraries and provides relevant code examples. We show that Geomstats provides reliable building blocks to foster research in differential geometry and statistics, and to democratize the use of Riemannian geometry in machine learning applications. The source code is freely available under the MIT license at \url{geomstats.ai}.