The Basic Geometric Structures of Electromagnetic Digital Information: Statistical characterization of the digital measurement of spatio-Doppler and polarimetric fluctuations of the radar electromagnetic wave

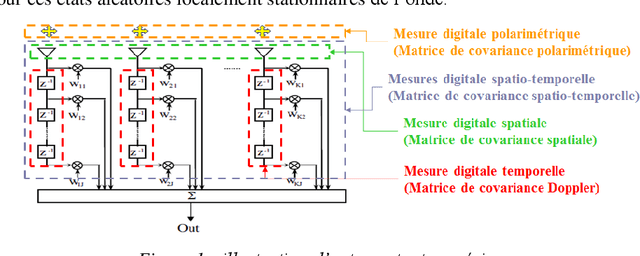
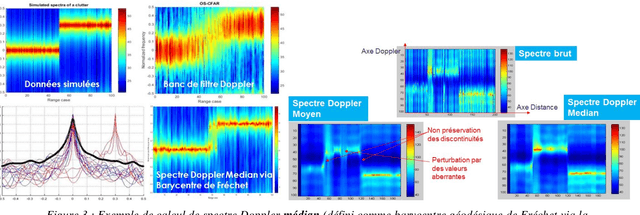
The aim is to describe new geometric approaches to define the statistics of spatio-temporal and polarimetric measurements of the states of an electromagnetic wave, using the works of Maurice Fr{\'e}chet, Jean-Louis Koszul and Jean-Marie Souriau, with in particular the notion of 'average' state of this digital measurement as a Fr{\'e}chet barycentre in a metric space and a model derived from statistical mechanics to define and calculate a maximum density of entropy (extension of the notion of Gaussian) to describe the fluctuations of the electromagnetic wave. The article will illustrate these new tools with examples of radar application for Doppler, spatio-temporal and polarimetric measurement of the electromagnetic wave by introducing a distance on the covariance matrices of the electromagnetic digital signal, based on Fisher's metric from Information Geometry.