Physics-model-guided Worst-case Sampling for Safe Reinforcement Learning

Real-world accidents in learning-enabled CPS frequently occur in challenging corner cases. During the training of deep reinforcement learning (DRL) policy, the standard setup for training conditions is either fixed at a single initial condition or uniformly sampled from the admissible state space. This setup often overlooks the challenging but safety-critical corner cases. To bridge this gap, this paper proposes a physics-model-guided worst-case sampling strategy for training safe policies that can handle safety-critical cases toward guaranteed safety. Furthermore, we integrate the proposed worst-case sampling strategy into the physics-regulated deep reinforcement learning (Phy-DRL) framework to build a more data-efficient and safe learning algorithm for safety-critical CPS. We validate the proposed training strategy with Phy-DRL through extensive experiments on a simulated cart-pole system, a 2D quadrotor, a simulated and a real quadruped robot, showing remarkably improved sampling efficiency to learn more robust safe policies.

Simplex-enabled Safe Continual Learning Machine

This paper proposes the SeC-Learning Machine: Simplex-enabled safe continual learning for safety-critical autonomous systems. The SeC-learning machine is built on Simplex logic (that is, ``using simplicity to control complexity'') and physics-regulated deep reinforcement learning (Phy-DRL). The SeC-learning machine thus constitutes HP (high performance)-Student, HA (high assurance)-Teacher, and Coordinator. Specifically, the HP-Student is a pre-trained high-performance but not fully verified Phy-DRL, continuing to learn in a real plant to tune the action policy to be safe. In contrast, the HA-Teacher is a mission-reduced, physics-model-based, and verified design. As a complementary, HA-Teacher has two missions: backing up safety and correcting unsafe learning. The Coordinator triggers the interaction and the switch between HP-Student and HA-Teacher. Powered by the three interactive components, the SeC-learning machine can i) assure lifetime safety (i.e., safety guarantee in any continual-learning stage, regardless of HP-Student's success or convergence), ii) address the Sim2Real gap, and iii) learn to tolerate unknown unknowns in real plants. The experiments on a cart-pole system and a real quadruped robot demonstrate the distinguished features of the SeC-learning machine, compared with continual learning built on state-of-the-art safe DRL frameworks with approaches to addressing the Sim2Real gap.

Physical Deep Reinforcement Learning: Safety and Unknown Unknowns

In this paper, we propose the Phy-DRL: a physics-model-regulated deep reinforcement learning framework for safety-critical autonomous systems. The Phy-DRL is unique in three innovations: i) proactive unknown-unknowns training, ii) conjunctive residual control (i.e., integration of data-driven control and physics-model-based control) and safety- \& stability-sensitive reward, and iii) physics-model-based neural network editing, including link editing and activation editing. Thanks to the concurrent designs, the Phy-DRL is able to 1) tolerate unknown-unknowns disturbances, 2) guarantee mathematically provable safety and stability, and 3) strictly comply with physical knowledge pertaining to Bellman equation and reward. The effectiveness of the Phy-DRL is finally validated by an inverted pendulum and a quadruped robot. The experimental results demonstrate that compared with purely data-driven DRL, Phy-DRL features remarkably fewer learning parameters, accelerated training and enlarged reward, while offering enhanced model robustness and safety assurance.

Physical Deep Reinforcement Learning Towards Safety Guarantee

Deep reinforcement learning (DRL) has achieved tremendous success in many complex decision-making tasks of autonomous systems with high-dimensional state and/or action spaces. However, the safety and stability still remain major concerns that hinder the applications of DRL to safety-critical autonomous systems. To address the concerns, we proposed the Phy-DRL: a physical deep reinforcement learning framework. The Phy-DRL is novel in two architectural designs: i) Lyapunov-like reward, and ii) residual control (i.e., integration of physics-model-based control and data-driven control). The concurrent physical reward and residual control empower the Phy-DRL the (mathematically) provable safety and stability guarantees. Through experiments on the inverted pendulum, we show that the Phy-DRL features guaranteed safety and stability and enhanced robustness, while offering remarkably accelerated training and enlarged reward.

Phy-Taylor: Physics-Model-Based Deep Neural Networks

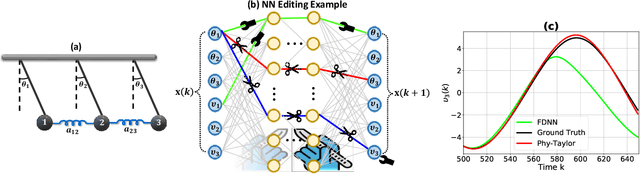
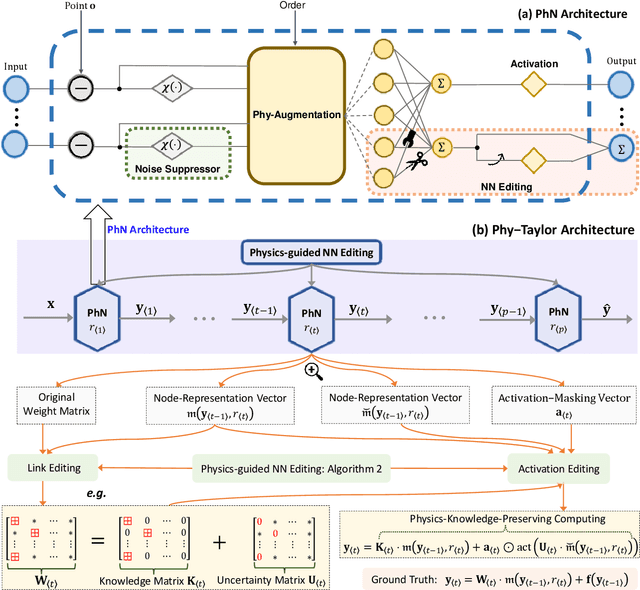
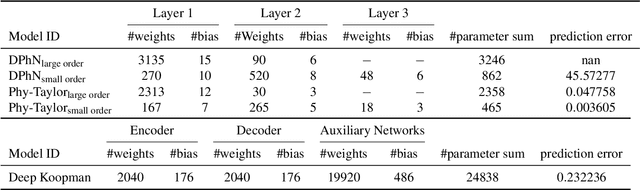
Purely data-driven deep neural networks (DNNs) applied to physical engineering systems can infer relations that violate physics laws, thus leading to unexpected consequences. To address this challenge, we propose a physics-model-based DNN framework, called Phy-Taylor, that accelerates learning compliant representations with physical knowledge. The Phy-Taylor framework makes two key contributions; it introduces a new architectural Physics-compatible neural network (PhN), and features a novel compliance mechanism, we call {\em Physics-guided Neural Network Editing\/}. The PhN aims to directly capture nonlinearities inspired by physical quantities, such as kinetic energy, potential energy, electrical power, and aerodynamic drag force. To do so, the PhN augments neural network layers with two key components: (i) monomials of Taylor series expansion of nonlinear functions capturing physical knowledge, and (ii) a suppressor for mitigating the influence of noise. The neural-network editing mechanism further modifies network links and activation functions consistently with physical knowledge. As an extension, we also propose a self-correcting Phy-Taylor framework that introduces two additional capabilities: (i) physics-model-based safety relationship learning, and (ii) automatic output correction when violations of safety occur. Through experiments, we show that (by expressing hard-to-learn nonlinearities directly and by constraining dependencies) Phy-Taylor features considerably fewer parameters, and a remarkably accelerated training process, while offering enhanced model robustness and accuracy.