Accurate and Scalable Graph Neural Networks via Message Invariance

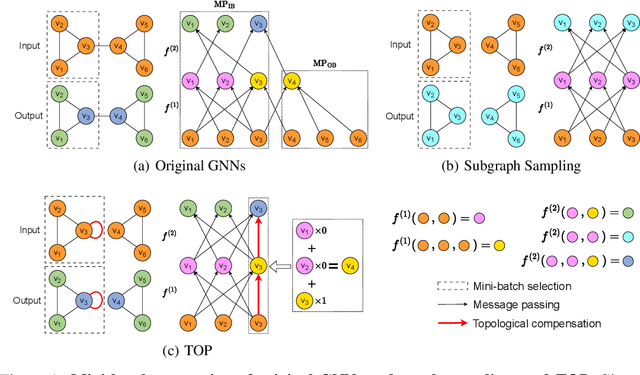
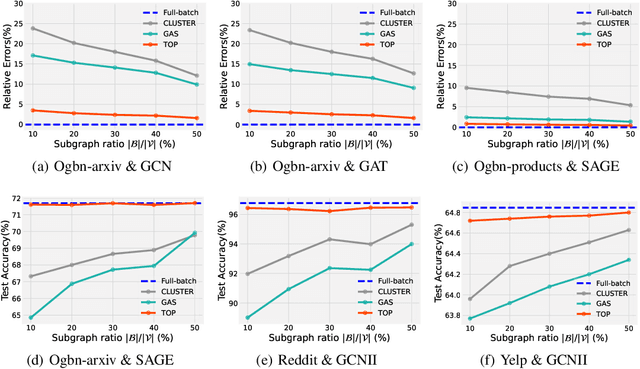
Message passing-based graph neural networks (GNNs) have achieved great success in many real-world applications. For a sampled mini-batch of target nodes, the message passing process is divided into two parts: message passing between nodes within the batch (MP-IB) and message passing from nodes outside the batch to those within it (MP-OB). However, MP-OB recursively relies on higher-order out-of-batch neighbors, leading to an exponentially growing computational cost with respect to the number of layers. Due to the neighbor explosion, the whole message passing stores most nodes and edges on the GPU such that many GNNs are infeasible to large-scale graphs. To address this challenge, we propose an accurate and fast mini-batch approach for large graph transductive learning, namely topological compensation (TOP), which obtains the outputs of the whole message passing solely through MP-IB, without the costly MP-OB. The major pillar of TOP is a novel concept of message invariance, which defines message-invariant transformations to convert costly MP-OB into fast MP-IB. This ensures that the modified MP-IB has the same output as the whole message passing. Experiments demonstrate that TOP is significantly faster than existing mini-batch methods by order of magnitude on vast graphs (millions of nodes and billions of edges) with limited accuracy degradation.

Robust Preference Optimization with Provable Noise Tolerance for LLMs

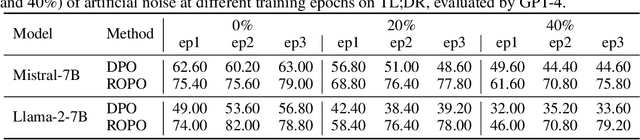
The preference alignment aims to enable large language models (LLMs) to generate responses that conform to human values, which is essential for developing general AI systems. Ranking-based methods -- a promising class of alignment approaches -- learn human preferences from datasets containing response pairs by optimizing the log-likelihood margins between preferred and dis-preferred responses. However, due to the inherent differences in annotators' preferences, ranking labels of comparisons for response pairs are unavoidably noisy. This seriously hurts the reliability of existing ranking-based methods. To address this problem, we propose a provably noise-tolerant preference alignment method, namely RObust Preference Optimization (ROPO). To the best of our knowledge, ROPO is the first preference alignment method with noise-tolerance guarantees. The key idea of ROPO is to dynamically assign conservative gradient weights to response pairs with high label uncertainty, based on the log-likelihood margins between the responses. By effectively suppressing the gradients of noisy samples, our weighting strategy ensures that the expected risk has the same gradient direction independent of the presence and proportion of noise. Experiments on three open-ended text generation tasks with four base models ranging in size from 2.8B to 13B demonstrate that ROPO significantly outperforms existing ranking-based methods.

Provably Convergent Subgraph-wise Sampling for Fast GNN Training

Subgraph-wise sampling -- a promising class of mini-batch training techniques for graph neural networks (GNNs -- is critical for real-world applications. During the message passing (MP) in GNNs, subgraph-wise sampling methods discard messages outside the mini-batches in backward passes to avoid the well-known neighbor explosion problem, i.e., the exponentially increasing dependencies of nodes with the number of MP iterations. However, discarding messages may sacrifice the gradient estimation accuracy, posing significant challenges to their convergence analysis and convergence speeds. To address this challenge, we propose a novel subgraph-wise sampling method with a convergence guarantee, namely Local Message Compensation (LMC). To the best of our knowledge, LMC is the first subgraph-wise sampling method with provable convergence. The key idea is to retrieve the discarded messages in backward passes based on a message passing formulation of backward passes. By efficient and effective compensations for the discarded messages in both forward and backward passes, LMC computes accurate mini-batch gradients and thus accelerates convergence. Moreover, LMC is applicable to various MP-based GNN architectures, including convolutional GNNs (finite message passing iterations with different layers) and recurrent GNNs (infinite message passing iterations with a shared layer). Experiments on large-scale benchmarks demonstrate that LMC is significantly faster than state-of-the-art subgraph-wise sampling methods.

LMC: Fast Training of GNNs via Subgraph Sampling with Provable Convergence

The message passing-based graph neural networks (GNNs) have achieved great success in many real-world applications. However, training GNNs on large-scale graphs suffers from the well-known neighbor explosion problem, i.e., the exponentially increasing dependencies of nodes with the number of message passing layers. Subgraph-wise sampling methods -- a promising class of mini-batch training techniques -- discard messages outside the mini-batches in backward passes to avoid the neighbor explosion problem at the expense of gradient estimation accuracy. This poses significant challenges to their convergence analysis and convergence speeds, which seriously limits their reliable real-world applications. To address this challenge, we propose a novel subgraph-wise sampling method with a convergence guarantee, namely Local Message Compensation (LMC). To the best of our knowledge, LMC is the {\it first} subgraph-wise sampling method with provable convergence. The key idea of LMC is to retrieve the discarded messages in backward passes based on a message passing formulation of backward passes. By efficient and effective compensations for the discarded messages in both forward and backward passes, LMC computes accurate mini-batch gradients and thus accelerates convergence. We further show that LMC converges to first-order stationary points of GNNs. Experiments on large-scale benchmark tasks demonstrate that LMC significantly outperforms state-of-the-art subgraph-wise sampling methods in terms of efficiency.