BEVPlace++: Fast, Robust, and Lightweight LiDAR Global Localization for Unmanned Ground Vehicles

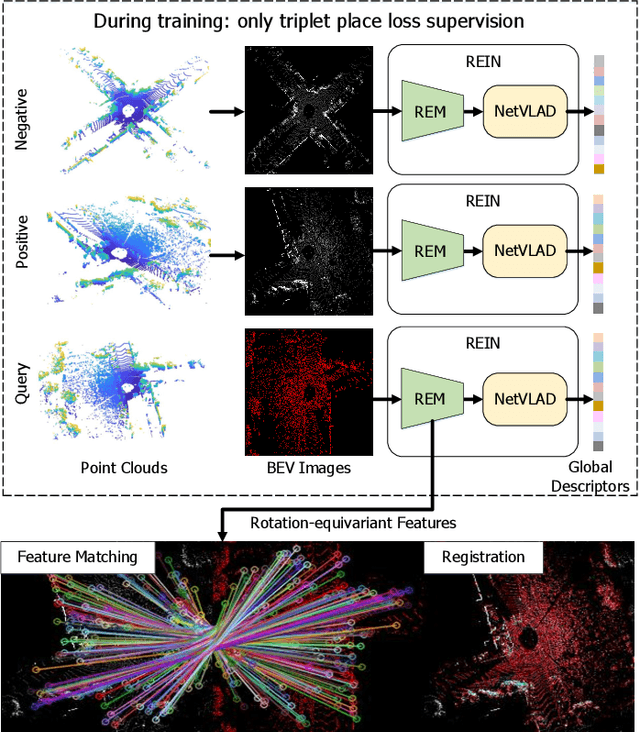
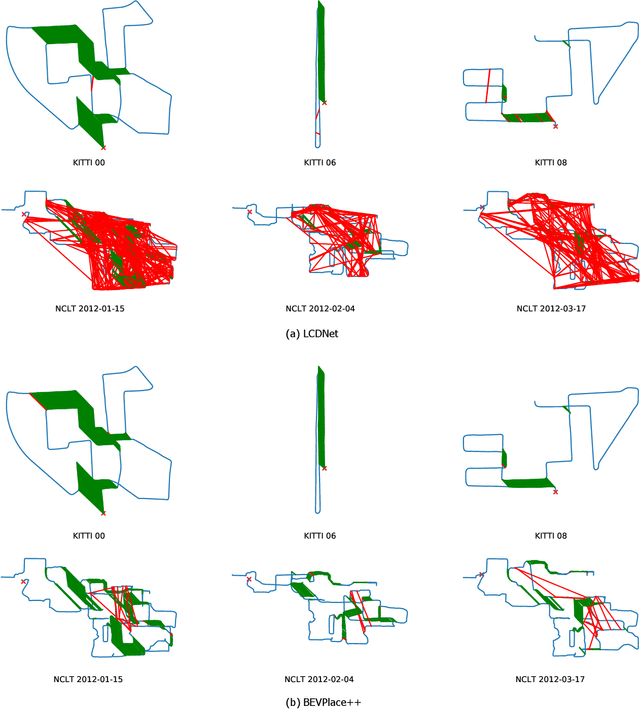
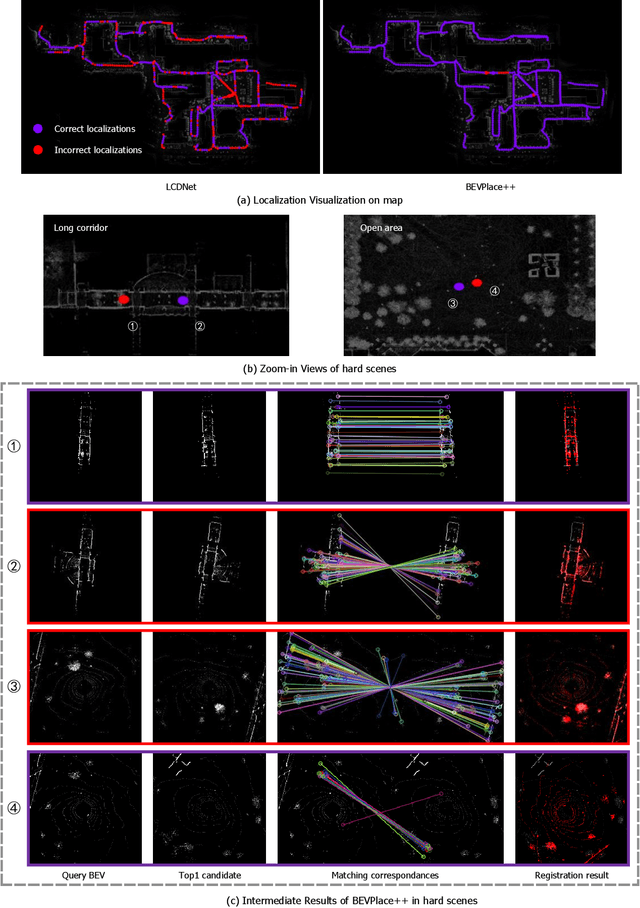
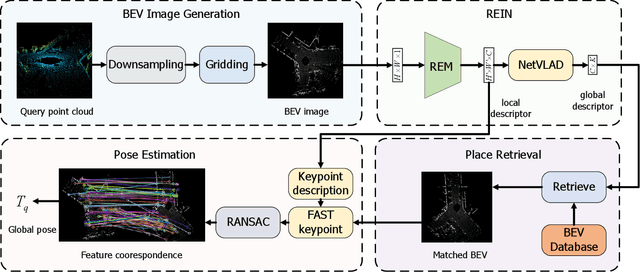
This article introduces BEVPlace++, a novel, fast, and robust LiDAR global localization method for unmanned ground vehicles. It uses lightweight convolutional neural networks (CNNs) on Bird's Eye View (BEV) image-like representations of LiDAR data to achieve accurate global localization through place recognition followed by 3-DoF pose estimation. Our detailed analyses reveal an interesting fact that CNNs are inherently effective at extracting distinctive features from LiDAR BEV images. Remarkably, keypoints of two BEV images with large translations can be effectively matched using CNN-extracted features. Building on this insight, we design a rotation equivariant module (REM) to obtain distinctive features while enhancing robustness to rotational changes. A Rotation Equivariant and Invariant Network (REIN) is then developed by cascading REM and a descriptor generator, NetVLAD, to sequentially generate rotation equivariant local features and rotation invariant global descriptors. The global descriptors are used first to achieve robust place recognition, and the local features are used for accurate pose estimation. Experimental results on multiple public datasets demonstrate that BEVPlace++, even when trained on a small dataset (3000 frames of KITTI) only with place labels, generalizes well to unseen environments, performs consistently across different days and years, and adapts to various types of LiDAR scanners. BEVPlace++ achieves state-of-the-art performance in subtasks of global localization including place recognition, loop closure detection, and global localization. Additionally, BEVPlace++ is lightweight, runs in real-time, and does not require accurate pose supervision, making it highly convenient for deployment. The source codes are publicly available at \href{https://github.com/zjuluolun/BEVPlace}{https://github.com/zjuluolun/BEVPlace}.

Sparse Recovery via Partial Regularization: Models, Theory and Algorithms

In the context of sparse recovery, it is known that most of existing regularizers such as $\ell_1$ suffer from some bias incurred by some leading entries (in magnitude) of the associated vector. To neutralize this bias, we propose a class of models with partial regularizers for recovering a sparse solution of a linear system. We show that every local minimizer of these models is sufficiently sparse or the magnitude of all its nonzero entries is above a uniform constant depending only on the data of the linear system. Moreover, for a class of partial regularizers, any global minimizer of these models is a sparsest solution to the linear system. We also establish some sufficient conditions for local or global recovery of the sparsest solution to the linear system, among which one of the conditions is weaker than the best known restricted isometry property (RIP) condition for sparse recovery by $\ell_1$. In addition, a first-order feasible augmented Lagrangian (FAL) method is proposed for solving these models, in which each subproblem is solved by a nonmonotone proximal gradient (NPG) method. Despite the complication of the partial regularizers, we show that each proximal subproblem in NPG can be solved as a certain number of one-dimensional optimization problems, which usually have a closed-form solution. We also show that any accumulation point of the sequence generated by FAL is a first-order stationary point of the models. Numerical results on compressed sensing and sparse logistic regression demonstrate that the proposed models substantially outperform the widely used ones in the literature in terms of solution quality.