Multilingual Clinical NER: Translation or Cross-lingual Transfer?

Natural language tasks like Named Entity Recognition (NER) in the clinical domain on non-English texts can be very time-consuming and expensive due to the lack of annotated data. Cross-lingual transfer (CLT) is a way to circumvent this issue thanks to the ability of multilingual large language models to be fine-tuned on a specific task in one language and to provide high accuracy for the same task in another language. However, other methods leveraging translation models can be used to perform NER without annotated data in the target language, by either translating the training set or test set. This paper compares cross-lingual transfer with these two alternative methods, to perform clinical NER in French and in German without any training data in those languages. To this end, we release MedNERF a medical NER test set extracted from French drug prescriptions and annotated with the same guidelines as an English dataset. Through extensive experiments on this dataset and on a German medical dataset (Frei and Kramer, 2021), we show that translation-based methods can achieve similar performance to CLT but require more care in their design. And while they can take advantage of monolingual clinical language models, those do not guarantee better results than large general-purpose multilingual models, whether with cross-lingual transfer or translation.

Quantitative Propagation of Chaos for SGD in Wide Neural Networks

In this paper, we investigate the limiting behavior of a continuous-time counterpart of the Stochastic Gradient Descent (SGD) algorithm applied to two-layer overparameterized neural networks, as the number or neurons (ie, the size of the hidden layer) $N \to +\infty$. Following a probabilistic approach, we show 'propagation of chaos' for the particle system defined by this continuous-time dynamics under different scenarios, indicating that the statistical interaction between the particles asymptotically vanishes. In particular, we establish quantitative convergence with respect to $N$ of any particle to a solution of a mean-field McKean-Vlasov equation in the metric space endowed with the Wasserstein distance. In comparison to previous works on the subject, we consider settings in which the sequence of stepsizes in SGD can potentially depend on the number of neurons and the iterations. We then identify two regimes under which different mean-field limits are obtained, one of them corresponding to an implicitly regularized version of the minimization problem at hand. We perform various experiments on real datasets to validate our theoretical results, assessing the existence of these two regimes on classification problems and illustrating our convergence results.

Continuous and Discrete-Time Analysis of Stochastic Gradient Descent for Convex and Non-Convex Functions

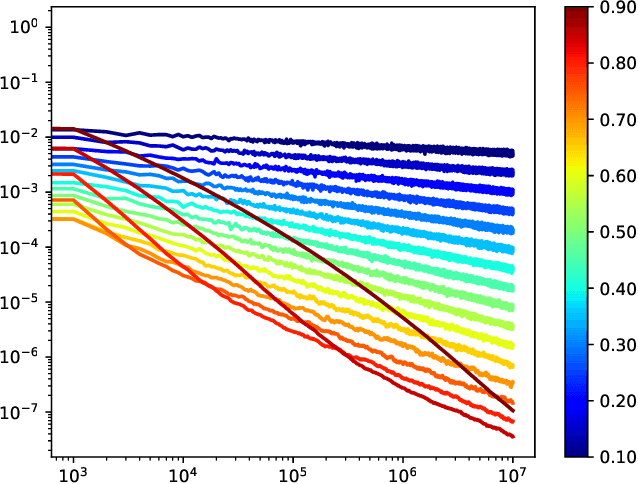
This paper proposes a thorough theoretical analysis of Stochastic Gradient Descent (SGD) with decreasing step sizes. First, we show that the recursion defining SGD can be provably approximated by solutions of a time inhomogeneous Stochastic Differential Equation (SDE) in a weak and strong sense. Then, motivated by recent analyses of deterministic and stochastic optimization methods by their continuous counterpart, we study the long-time convergence of the continuous processes at hand and establish non-asymptotic bounds. To that purpose, we develop new comparison techniques which we think are of independent interest. This continuous analysis allows us to develop an intuition on the convergence of SGD and, adapting the technique to the discrete setting, we show that the same results hold to the corresponding sequences. In our analysis, we notably obtain non-asymptotic bounds in the convex setting for SGD under weaker assumptions than the ones considered in previous works. Finally, we also establish finite time convergence results under various conditions, including relaxations of the famous {\L}ojasiewicz inequality, which can be applied to a class of non-convex functions.

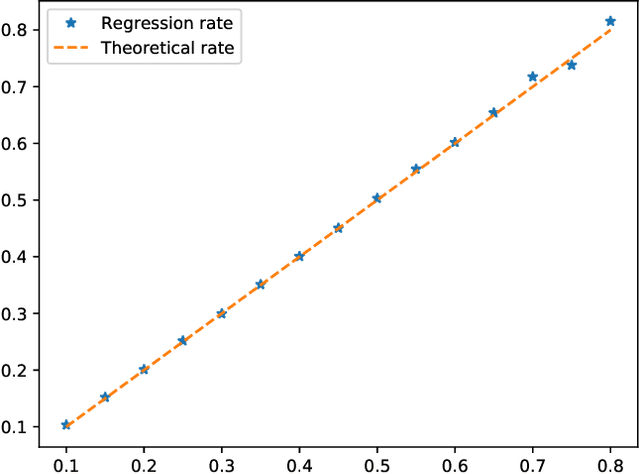
Active Linear Regression

We consider the problem of active linear regression where a decision maker has to choose between several covariates to sample in order to obtain the best estimate $\hat{\beta}$ of the parameter $\beta^{\star}$ of the linear model, in the sense of minimizing $\mathbb{E} \lVert\hat{\beta}-\beta^{\star}\rVert^2$. Using bandit and convex optimization techniques we propose an algorithm to define the sampling strategy of the decision maker and we compare it with other algorithms. We provide theoretical guarantees of our algorithm in different settings, including a $\mathcal{O}(T^{-2})$ regret bound in the case where the covariates form a basis of the feature space, generalizing and improving existing results. Numerical experiments validate our theoretical findings.

A Problem-Adaptive Algorithm for Resource Allocation

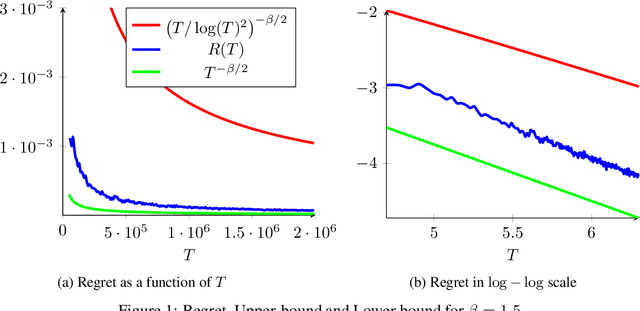
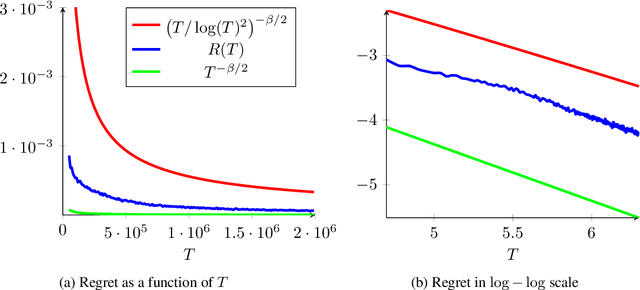
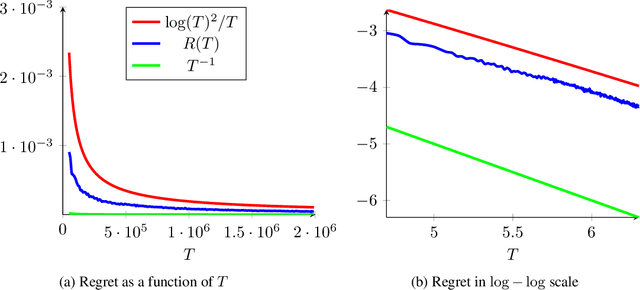
We consider a sequential stochastic resource allocation problem under the gradient feedback, where the reward of each resource is concave. We construct a generic algorithm that is adaptive to the complexity of the problem, which is measured using the exponent in {\L}ojasiewicz inequality. Our algorithm interpolates between the non-strongly concave and the strongly-concave rates without depending on the strong-concavity parameter and recover the fast rate of classical multi-armed bandit (corresponding roughly to linear reward functions).

Regularized Contextual Bandits

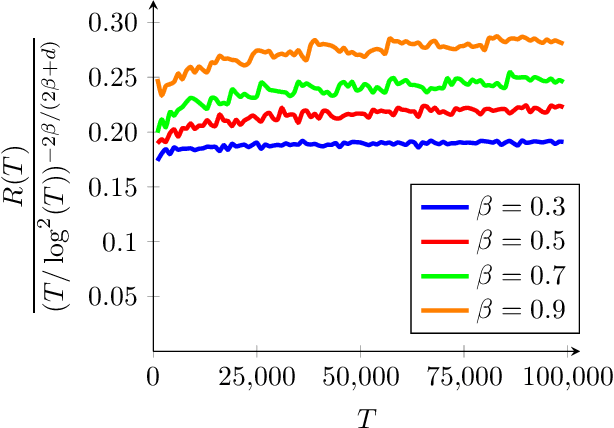
We consider the stochastic contextual bandit problem with additional regularization. The motivation comes from problems where the policy of the agent must be close to some baseline policy which is known to perform well on the task. To tackle this problem we use a nonparametric model and propose an algorithm splitting the context space into bins, and solving simultaneously - and independently - regularized multi-armed bandit instances on each bin. We derive slow and fast rates of convergence, depending on the unknown complexity of the problem. We also consider a new relevant margin condition to get problem-independent convergence rates, ending up in intermediate convergence rates interpolating between the aforementioned slow and fast rates.