A Problem-Adaptive Algorithm for Resource Allocation
Paper and Code
Feb 12, 2019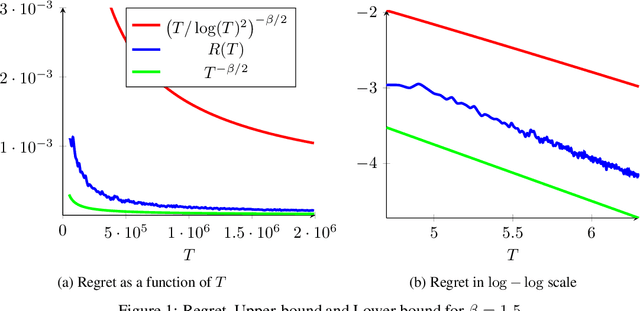
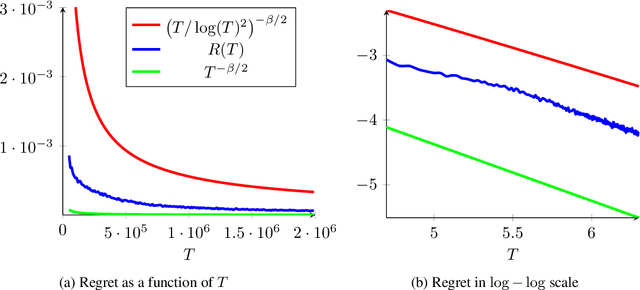
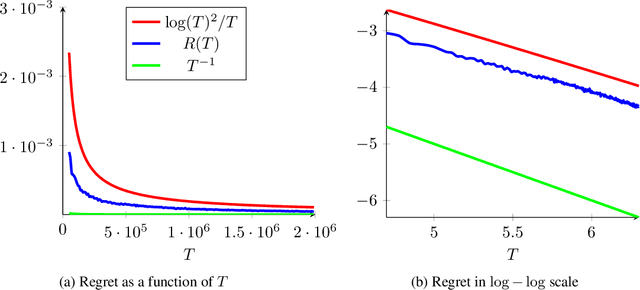

We consider a sequential stochastic resource allocation problem under the gradient feedback, where the reward of each resource is concave. We construct a generic algorithm that is adaptive to the complexity of the problem, which is measured using the exponent in {\L}ojasiewicz inequality. Our algorithm interpolates between the non-strongly concave and the strongly-concave rates without depending on the strong-concavity parameter and recover the fast rate of classical multi-armed bandit (corresponding roughly to linear reward functions).
* 34 pages, 9 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge