Regularized Contextual Bandits
Paper and Code
Oct 11, 2018

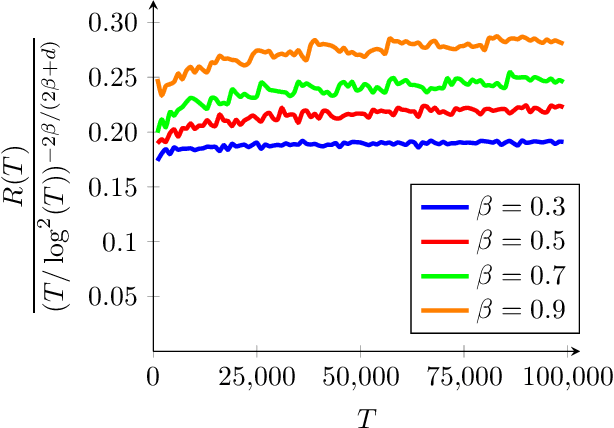
We consider the stochastic contextual bandit problem with additional regularization. The motivation comes from problems where the policy of the agent must be close to some baseline policy which is known to perform well on the task. To tackle this problem we use a nonparametric model and propose an algorithm splitting the context space into bins, and solving simultaneously - and independently - regularized multi-armed bandit instances on each bin. We derive slow and fast rates of convergence, depending on the unknown complexity of the problem. We also consider a new relevant margin condition to get problem-independent convergence rates, ending up in intermediate convergence rates interpolating between the aforementioned slow and fast rates.
* 31 pages, 2 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge