Wing Tat Leung
Learning-based Multi-continuum Model for Multiscale Flow Problems
Mar 21, 2024Abstract:Multiscale problems can usually be approximated through numerical homogenization by an equation with some effective parameters that can capture the macroscopic behavior of the original system on the coarse grid to speed up the simulation. However, this approach usually assumes scale separation and that the heterogeneity of the solution can be approximated by the solution average in each coarse block. For complex multiscale problems, the computed single effective properties/continuum might be inadequate. In this paper, we propose a novel learning-based multi-continuum model to enrich the homogenized equation and improve the accuracy of the single continuum model for multiscale problems with some given data. Without loss of generalization, we consider a two-continuum case. The first flow equation keeps the information of the original homogenized equation with an additional interaction term. The second continuum is newly introduced, and the effective permeability in the second flow equation is determined by a neural network. The interaction term between the two continua aligns with that used in the Dual-porosity model but with a learnable coefficient determined by another neural network. The new model with neural network terms is then optimized using trusted data. We discuss both direct back-propagation and the adjoint method for the PDE-constraint optimization problem. Our proposed learning-based multi-continuum model can resolve multiple interacted media within each coarse grid block and describe the mass transfer among them, and it has been demonstrated to significantly improve the simulation results through numerical experiments involving both linear and nonlinear flow equations.
AMS-Net: Adaptive Multiscale Sparse Neural Network with Interpretable Basis Expansion for Multiphase Flow Problems
Jul 24, 2022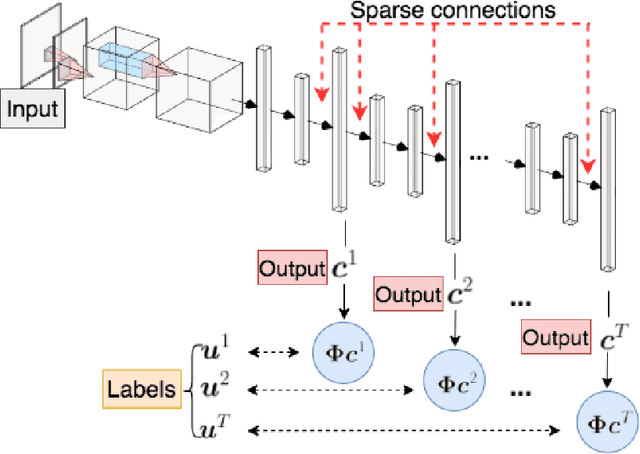
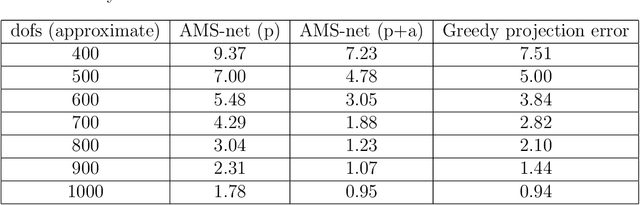
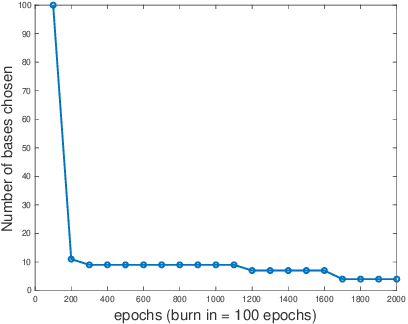
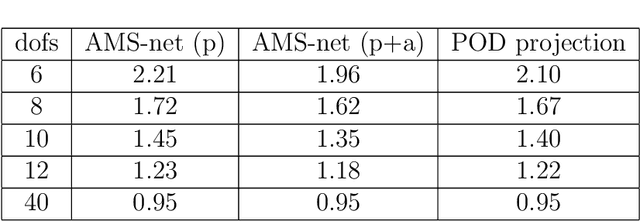
Abstract:In this work, we propose an adaptive sparse learning algorithm that can be applied to learn the physical processes and obtain a sparse representation of the solution given a large snapshot space. Assume that there is a rich class of precomputed basis functions that can be used to approximate the quantity of interest. We then design a neural network architecture to learn the coefficients of solutions in the spaces which are spanned by these basis functions. The information of the basis functions are incorporated in the loss function, which minimizes the differences between the downscaled reduced order solutions and reference solutions at multiple time steps. The network contains multiple submodules and the solutions at different time steps can be learned simultaneously. We propose some strategies in the learning framework to identify important degrees of freedom. To find a sparse solution representation, a soft thresholding operator is applied to enforce the sparsity of the output coefficient vectors of the neural network. To avoid over-simplification and enrich the approximation space, some degrees of freedom can be added back to the system through a greedy algorithm. In both scenarios, that is, removing and adding degrees of freedom, the corresponding network connections are pruned or reactivated guided by the magnitude of the solution coefficients obtained from the network outputs. The proposed adaptive learning process is applied to some toy case examples to demonstrate that it can achieve a good basis selection and accurate approximation. More numerical tests are performed on two-phase multiscale flow problems to show the capability and interpretability of the proposed method on complicated applications.
Multi-agent Reinforcement Learning Accelerated MCMC on Multiscale Inversion Problem
Nov 17, 2020
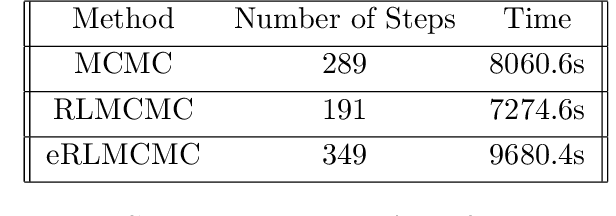
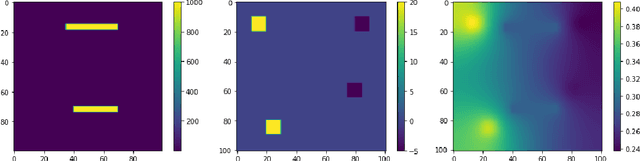

Abstract:In this work, we propose a multi-agent actor-critic reinforcement learning (RL) algorithm to accelerate the multi-level Monte Carlo Markov Chain (MCMC) sampling algorithms. The policies (actors) of the agents are used to generate the proposal in the MCMC steps; and the critic, which is centralized, is in charge of estimating the long term reward. We verify our proposed algorithm by solving an inverse problem with multiple scales. There are several difficulties in the implementation of this problem by using traditional MCMC sampling. Firstly, the computation of the posterior distribution involves evaluating the forward solver, which is very time consuming for a problem with heterogeneous. We hence propose to use the multi-level algorithm. More precisely, we use the generalized multiscale finite element method (GMsFEM) as the forward solver in evaluating a posterior distribution in the multi-level rejection procedure. Secondly, it is hard to find a function which can generate samplings which are meaningful. To solve this issue, we learn an RL policy as the proposal generator. Our experiments show that the proposed method significantly improves the sampling process
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge