AMS-Net: Adaptive Multiscale Sparse Neural Network with Interpretable Basis Expansion for Multiphase Flow Problems
Paper and Code
Jul 24, 2022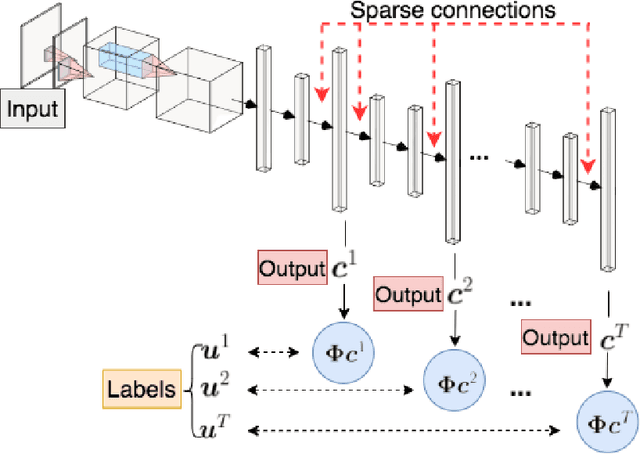
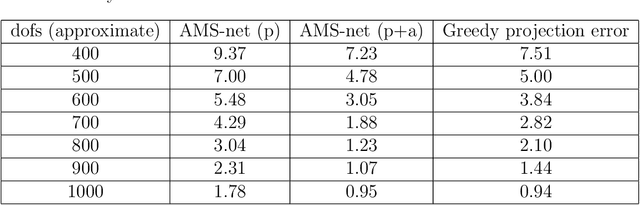
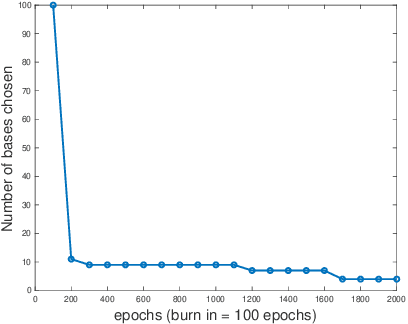
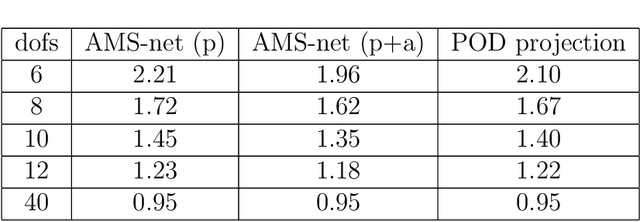
In this work, we propose an adaptive sparse learning algorithm that can be applied to learn the physical processes and obtain a sparse representation of the solution given a large snapshot space. Assume that there is a rich class of precomputed basis functions that can be used to approximate the quantity of interest. We then design a neural network architecture to learn the coefficients of solutions in the spaces which are spanned by these basis functions. The information of the basis functions are incorporated in the loss function, which minimizes the differences between the downscaled reduced order solutions and reference solutions at multiple time steps. The network contains multiple submodules and the solutions at different time steps can be learned simultaneously. We propose some strategies in the learning framework to identify important degrees of freedom. To find a sparse solution representation, a soft thresholding operator is applied to enforce the sparsity of the output coefficient vectors of the neural network. To avoid over-simplification and enrich the approximation space, some degrees of freedom can be added back to the system through a greedy algorithm. In both scenarios, that is, removing and adding degrees of freedom, the corresponding network connections are pruned or reactivated guided by the magnitude of the solution coefficients obtained from the network outputs. The proposed adaptive learning process is applied to some toy case examples to demonstrate that it can achieve a good basis selection and accurate approximation. More numerical tests are performed on two-phase multiscale flow problems to show the capability and interpretability of the proposed method on complicated applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge