Multi-agent Reinforcement Learning Accelerated MCMC on Multiscale Inversion Problem

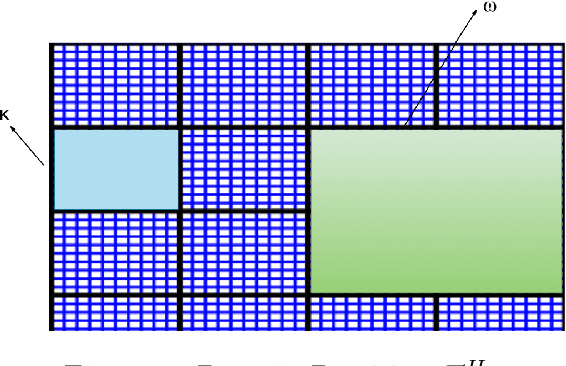
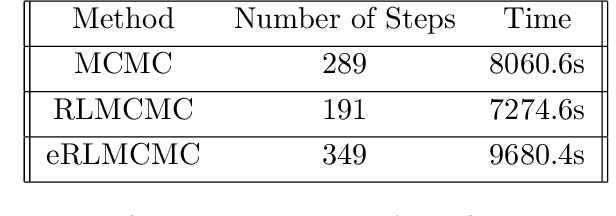
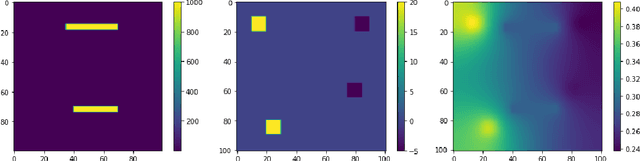
In this work, we propose a multi-agent actor-critic reinforcement learning (RL) algorithm to accelerate the multi-level Monte Carlo Markov Chain (MCMC) sampling algorithms. The policies (actors) of the agents are used to generate the proposal in the MCMC steps; and the critic, which is centralized, is in charge of estimating the long term reward. We verify our proposed algorithm by solving an inverse problem with multiple scales. There are several difficulties in the implementation of this problem by using traditional MCMC sampling. Firstly, the computation of the posterior distribution involves evaluating the forward solver, which is very time consuming for a problem with heterogeneous. We hence propose to use the multi-level algorithm. More precisely, we use the generalized multiscale finite element method (GMsFEM) as the forward solver in evaluating a posterior distribution in the multi-level rejection procedure. Secondly, it is hard to find a function which can generate samplings which are meaningful. To solve this issue, we learn an RL policy as the proposal generator. Our experiments show that the proposed method significantly improves the sampling process

Deep Multiscale Model Learning

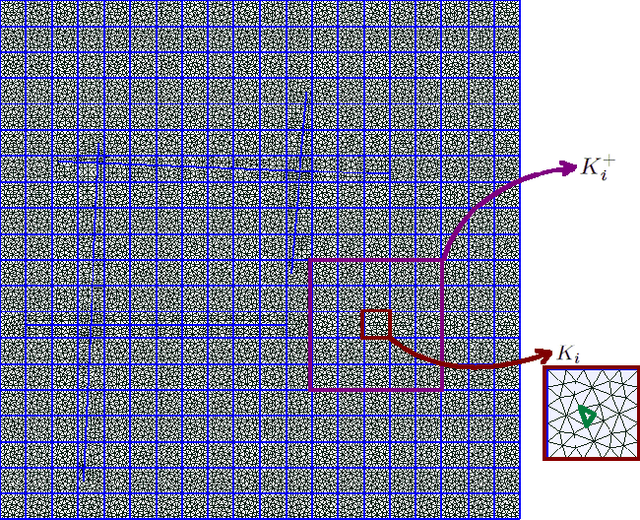
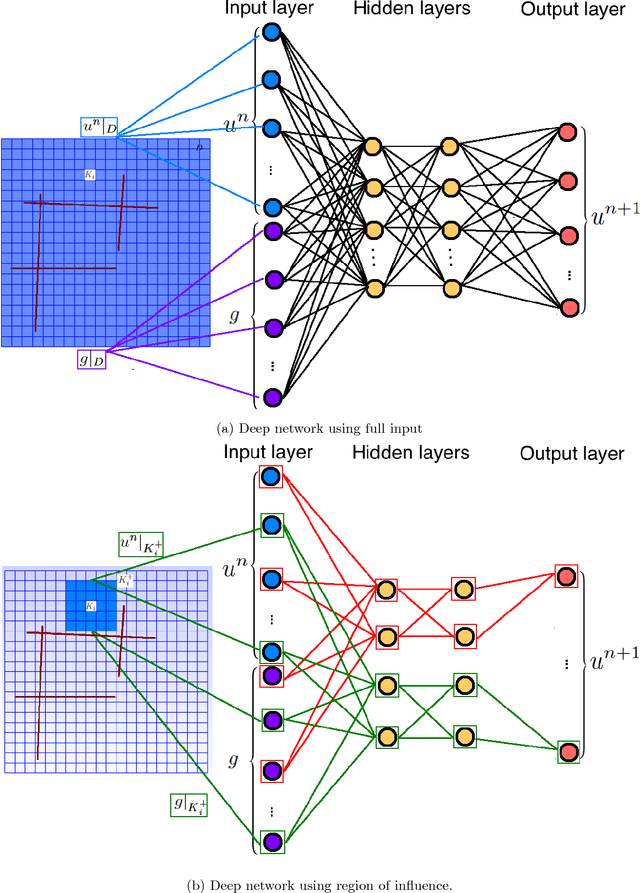
The objective of this paper is to design novel multi-layer neural network architectures for multiscale simulations of flows taking into account the observed data and physical modeling concepts. Our approaches use deep learning concepts combined with local multiscale model reduction methodologies to predict flow dynamics. Using reduced-order model concepts is important for constructing robust deep learning architectures since the reduced-order models provide fewer degrees of freedom. Flow dynamics can be thought of as multi-layer networks. More precisely, the solution (e.g., pressures and saturations) at the time instant $n+1$ depends on the solution at the time instant $n$ and input parameters, such as permeability fields, forcing terms, and initial conditions. One can regard the solution as a multi-layer network, where each layer, in general, is a nonlinear forward map and the number of layers relates to the internal time steps. We will rely on rigorous model reduction concepts to define unknowns and connections for each layer. In each layer, our reduced-order models will provide a forward map, which will be modified ("trained") using available data. It is critical to use reduced-order models for this purpose, which will identify the regions of influence and the appropriate number of variables. Because of the lack of available data, the training will be supplemented with computational data as needed and the interpolation between data-rich and data-deficient models. We will also use deep learning algorithms to train the elements of the reduced model discrete system. We will present main ingredients of our approach and numerical results. Numerical results show that using deep learning and multiscale models, we can improve the forward models, which are conditioned to the available data.