William Bialek
NEC Research Institute
Moving boundaries: An appreciation of John Hopfield
Dec 23, 2024


Abstract:The 2024 Nobel Prize in Physics was awarded to John Hopfield and Geoffrey Hinton, "for foundational discoveries and inventions that enable machine learning with artificial neural networks." As noted by the Nobel committee, their work moved the boundaries of physics. This is a brief reflection on Hopfield's work, its implications for the emergence of biological physics as a part of physics, the path from his early papers to the modern revolution in artificial intelligence, and prospects for the future.
Mapping the stereotyped behaviour of freely-moving fruit flies
Aug 12, 2014

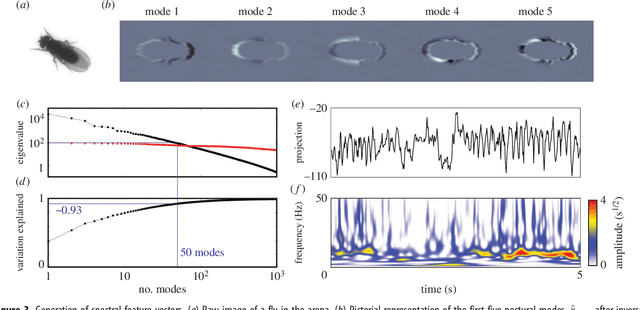

Abstract:Most animals possess the ability to actuate a vast diversity of movements, ostensibly constrained only by morphology and physics. In practice, however, a frequent assumption in behavioral science is that most of an animal's activities can be described in terms of a small set of stereotyped motifs. Here we introduce a method for mapping the behavioral space of organisms, relying only upon the underlying structure of postural movement data to organize and classify behaviors. We find that six different drosophilid species each perform a mix of non-stereotyped actions and over one hundred hierarchically-organized, stereotyped behaviors. Moreover, we use this approach to compare these species' behavioral spaces, systematically identifying subtle behavioral differences between closely-related species.
Toward a statistical mechanics of four letter words
Dec 31, 2007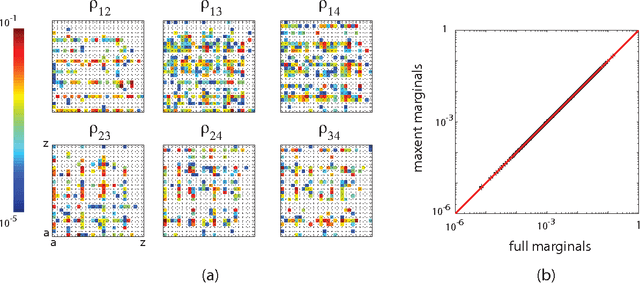
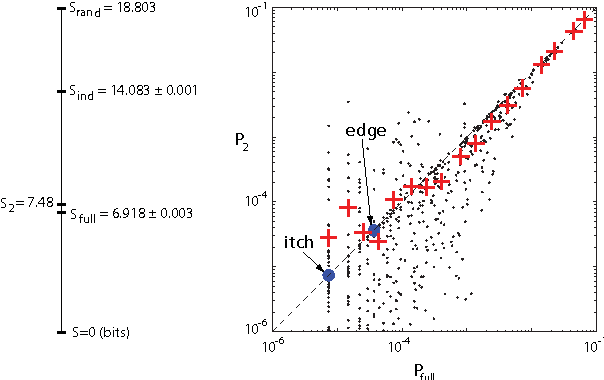


Abstract:We consider words as a network of interacting letters, and approximate the probability distribution of states taken on by this network. Despite the intuition that the rules of English spelling are highly combinatorial (and arbitrary), we find that maximum entropy models consistent with pairwise correlations among letters provide a surprisingly good approximation to the full statistics of four letter words, capturing ~92% of the multi-information among letters and even "discovering" real words that were not represented in the data from which the pairwise correlations were estimated. The maximum entropy model defines an energy landscape on the space of possible words, and local minima in this landscape account for nearly two-thirds of words used in written English.
Estimating mutual information and multi--information in large networks
Feb 03, 2005


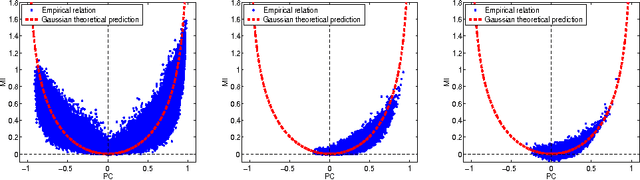
Abstract:We address the practical problems of estimating the information relations that characterize large networks. Building on methods developed for analysis of the neural code, we show that reliable estimates of mutual information can be obtained with manageable computational effort. The same methods allow estimation of higher order, multi--information terms. These ideas are illustrated by analyses of gene expression, financial markets, and consumer preferences. In each case, information theoretic measures correlate with independent, intuitive measures of the underlying structures in the system.
Occam factors and model-independent Bayesian learning of continuous distributions
Feb 05, 2002

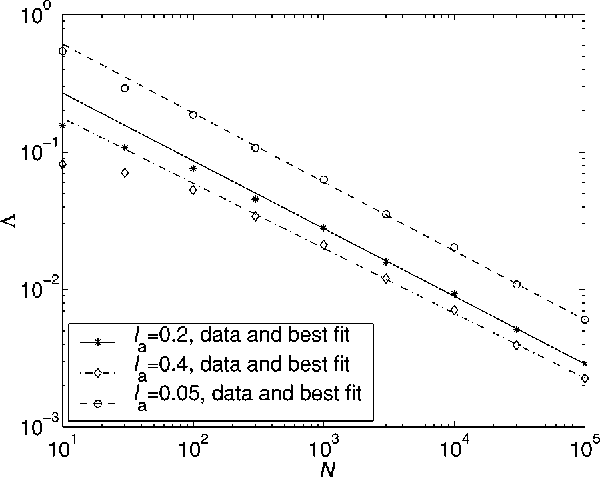
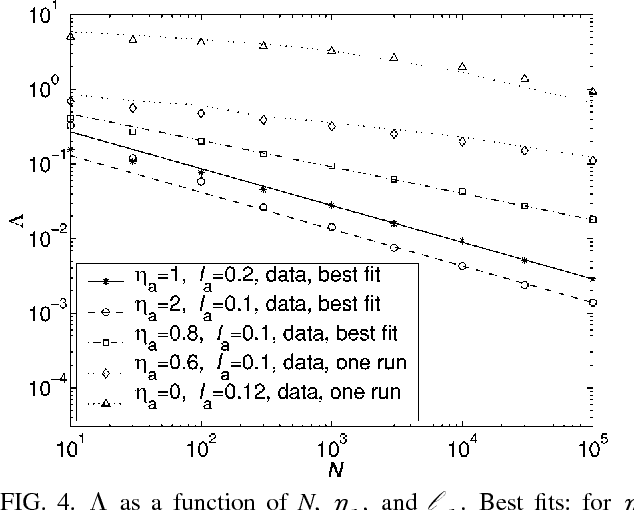
Abstract:Learning of a smooth but nonparametric probability density can be regularized using methods of Quantum Field Theory. We implement a field theoretic prior numerically, test its efficacy, and show that the data and the phase space factors arising from the integration over the model space determine the free parameter of the theory ("smoothness scale") self-consistently. This persists even for distributions that are atypical in the prior and is a step towards a model-independent theory for learning continuous distributions. Finally, we point out that a wrong parameterization of a model family may sometimes be advantageous for small data sets.
* publication revisions: extended introduction, new references, other minor corrections; 6 pages, 6 figures, revtex
Predictability, complexity and learning
Jan 23, 2001Abstract:We define {\em predictive information} $I_{\rm pred} (T)$ as the mutual information between the past and the future of a time series. Three qualitatively different behaviors are found in the limit of large observation times $T$: $I_{\rm pred} (T)$ can remain finite, grow logarithmically, or grow as a fractional power law. If the time series allows us to learn a model with a finite number of parameters, then $I_{\rm pred} (T)$ grows logarithmically with a coefficient that counts the dimensionality of the model space. In contrast, power--law growth is associated, for example, with the learning of infinite parameter (or nonparametric) models such as continuous functions with smoothness constraints. There are connections between the predictive information and measures of complexity that have been defined both in learning theory and in the analysis of physical systems through statistical mechanics and dynamical systems theory. Further, in the same way that entropy provides the unique measure of available information consistent with some simple and plausible conditions, we argue that the divergent part of $I_{\rm pred} (T)$ provides the unique measure for the complexity of dynamics underlying a time series. Finally, we discuss how these ideas may be useful in different problems in physics, statistics, and biology.
* 53 pages, 3 figures, 98 references, LaTeX2e
The information bottleneck method
Apr 24, 2000Abstract:We define the relevant information in a signal $x\in X$ as being the information that this signal provides about another signal $y\in \Y$. Examples include the information that face images provide about the names of the people portrayed, or the information that speech sounds provide about the words spoken. Understanding the signal $x$ requires more than just predicting $y$, it also requires specifying which features of $\X$ play a role in the prediction. We formalize this problem as that of finding a short code for $\X$ that preserves the maximum information about $\Y$. That is, we squeeze the information that $\X$ provides about $\Y$ through a `bottleneck' formed by a limited set of codewords $\tX$. This constrained optimization problem can be seen as a generalization of rate distortion theory in which the distortion measure $d(x,\x)$ emerges from the joint statistics of $\X$ and $\Y$. This approach yields an exact set of self consistent equations for the coding rules $X \to \tX$ and $\tX \to \Y$. Solutions to these equations can be found by a convergent re-estimation method that generalizes the Blahut-Arimoto algorithm. Our variational principle provides a surprisingly rich framework for discussing a variety of problems in signal processing and learning, as will be described in detail elsewhere.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge